| Euclid of Alexandria (200 BC) Greek
Archimedes of Syracuse (287 – 212 BC) Greek
Apollonius of Perga (262 – 190 BC) Greek
Marcus Vitruvius Pollio (80 – 70 BC) Roman
Anthemius of Tralles (474 – 558) Greek - Roman
Abul Wafa al-Buzjani (940 – 998) Persian, Baghdad
Villard de Honnecourt (1225) Cistercian Order of France
Matthäus Roritzer (1435 – 1495) German
Albrecht Dürer (1471 – 1528) German
Rodrigo Gil (1500 – 1577) Spanish
Andrea Palladio (1508 – 1580) French
Philibert De l'Orme, (1515 – 1576) French
Francois Derand (1588 – 1644) French
Mathurin Jousse(1607 – 1692) French
Gérard Desargues(1591 – 1661) French
Amédée-François Frézier(1682 – 1773)
French
Gaspard Monge (1746 – 1818) French
Peter Nicholson (1765–1844) British
Asher Benjamin (1773 – 1845) American
Robert Willis (1800 – 1875) British
Last summer I became interested in medieval Gothic cross ribbed vaulting
after reading and seeing “Pillars of the Earth”, by Ken
Follett. I wanted to know if the Medieval thru Renaissance builders
used a trammel or a rope to draw out the ellipses of the cross vaults.
Or did they use ordinates to transfer the points of the circles (major/minor)
to points on the ellipse? What I ended up getting was a history lessons
in geometry. I ended up with more questions, than answers to my question.
The following is a brief summary of the history lesson I got in geometry.
A Gothic vault is composed of ribs, keystones and webs (curved masonry
that fills the web between ribs). The ribs are the cross vault diagonals,
transverse ribs and the wall ribs.
There are hundreds, if not thousands of architectural historians over
the last two hundred years who have basically asked the same question.
Or more importantly, how did the medieval cathedrals get built. A lot
of the architectural historians provide a good insight into the building
of the cathedrals, but in the end their findings are speculative. Do
to the lack of documentation on the medieval construction techniques.
As a carpenter-builder I've read a couple hundred documents, thesis
and books by the architectural historians and my findings are as speculative
as theirs, but thru the eyes of a carpenter who uses a lot of the same
building techniques as the medieval carpenters did 1000 years ago.
I’ll start with “the following diagram is self-evident
and needs no further explanation”. I’ve read the self-evident
statement in several of the “Carpentry and Building Journals”
published from 1880 to 1905. It also appears in most of the books written
on carpentry from 1800 to 1900. What the writer’s were really
saying was that they were expressing postulates just like Euclid that
were self-evident. There are really only two postulates from the Euclid's
Elements that we need to know as carpenters to end all of our paragraphs
with “it is self-evident and needs no further explanation”.
The two postulates are Euclid’s Elements Book 1 Prop 1 and Euclid's
Elements Book 1 Prop 47.
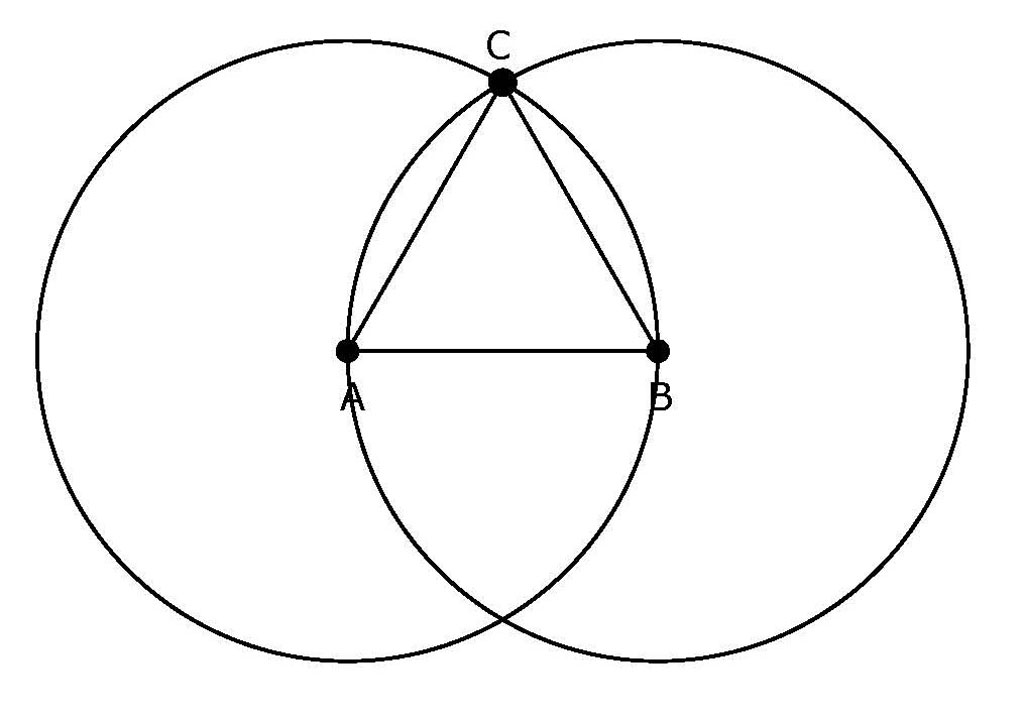
Euclid's Elements Book 1 Prop 1, to construct an equilateral triangle on a
given finite straight line A-B. The radius of the circles are AB. The equilateral
triangle ACB is form by the intersection of the two circles.
This is the basic geometric figure that 100’s of other geometric
figures can be drawn from. Two easy examples that we use as carpenters
are the equilateral arch and the Gothic Arch.
Equilateral Arch from Euclid’s Elements Book 1 Prop 1.
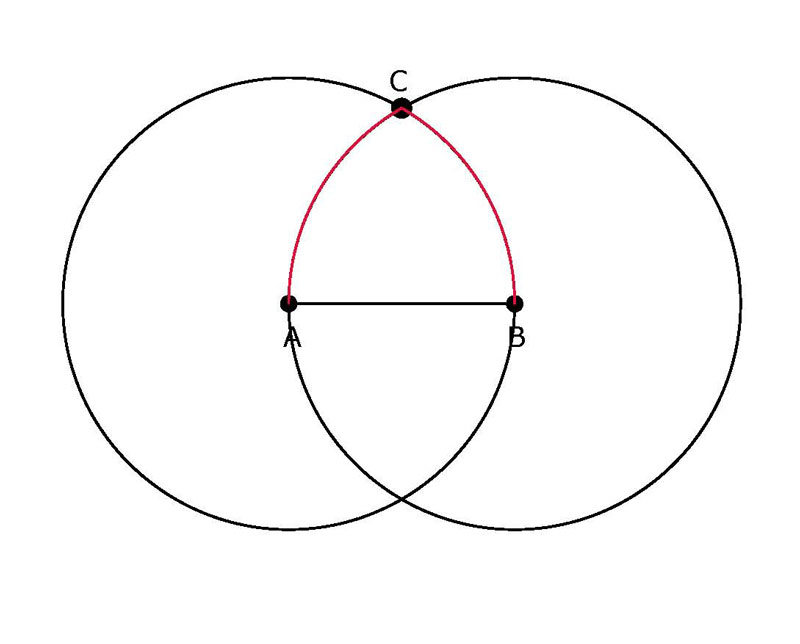
Gothic Arch from Euclid's Elements Book 1 Prop 1.
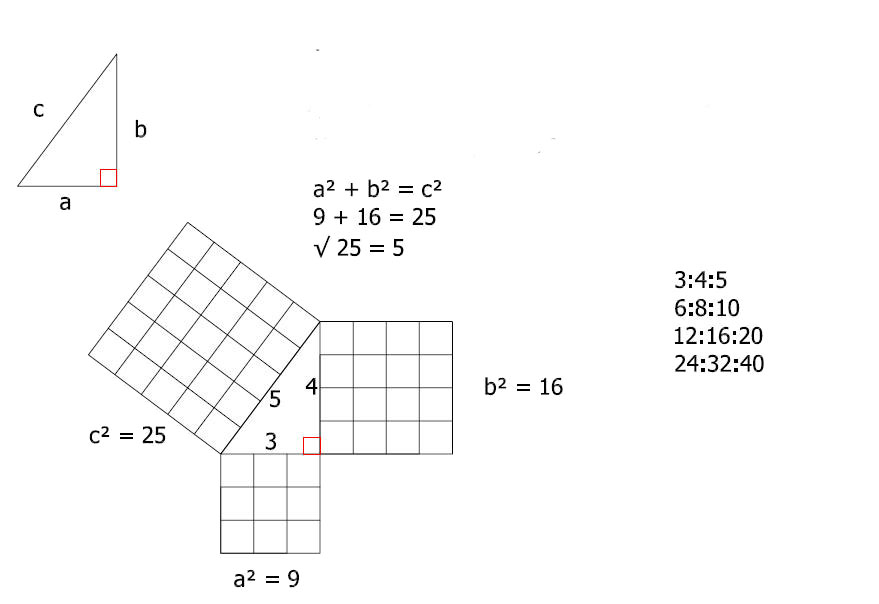
Euclid's Elements Book 1 Prop 47. In right-angled triangles the square
on the side opposite the right angle equals the sum of the squares
on the sides containing the right angle. We've all been there done
that with the Pythagoras theorem, but it's neat to count the squares
so we can say "it is self-evident and needs no further explanation".
From Euclid's Elements Book 1 Prop 1, to construct an equilateral triangle
you can easily create 100’s six point geometric figures.
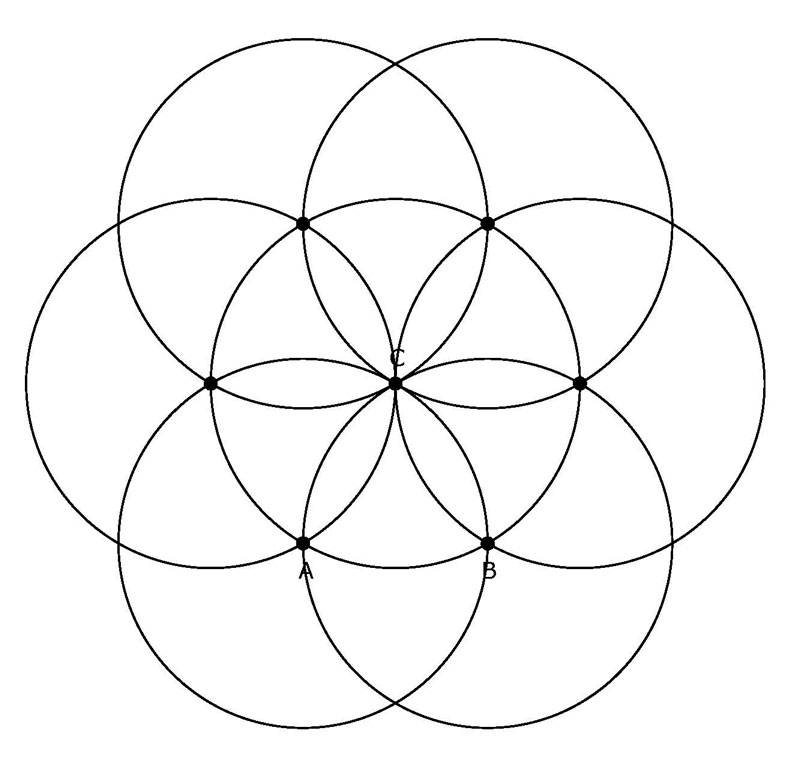
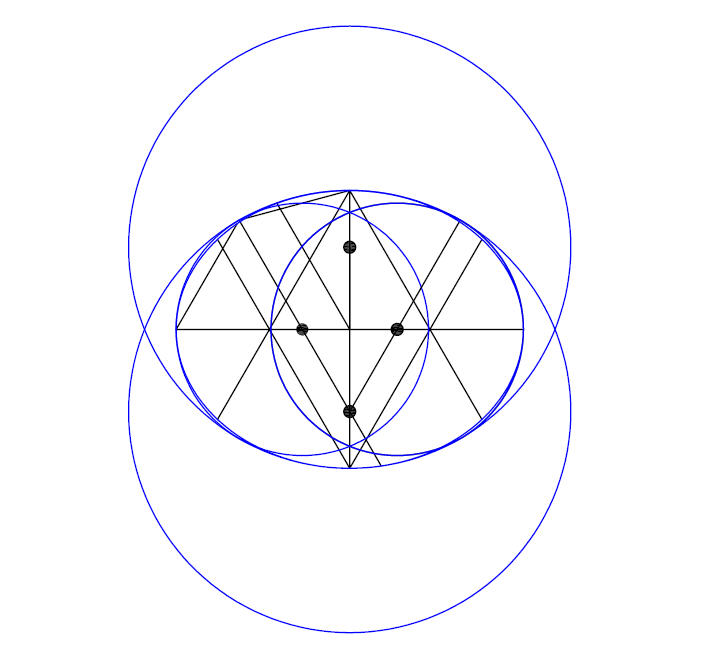
Seed of Life
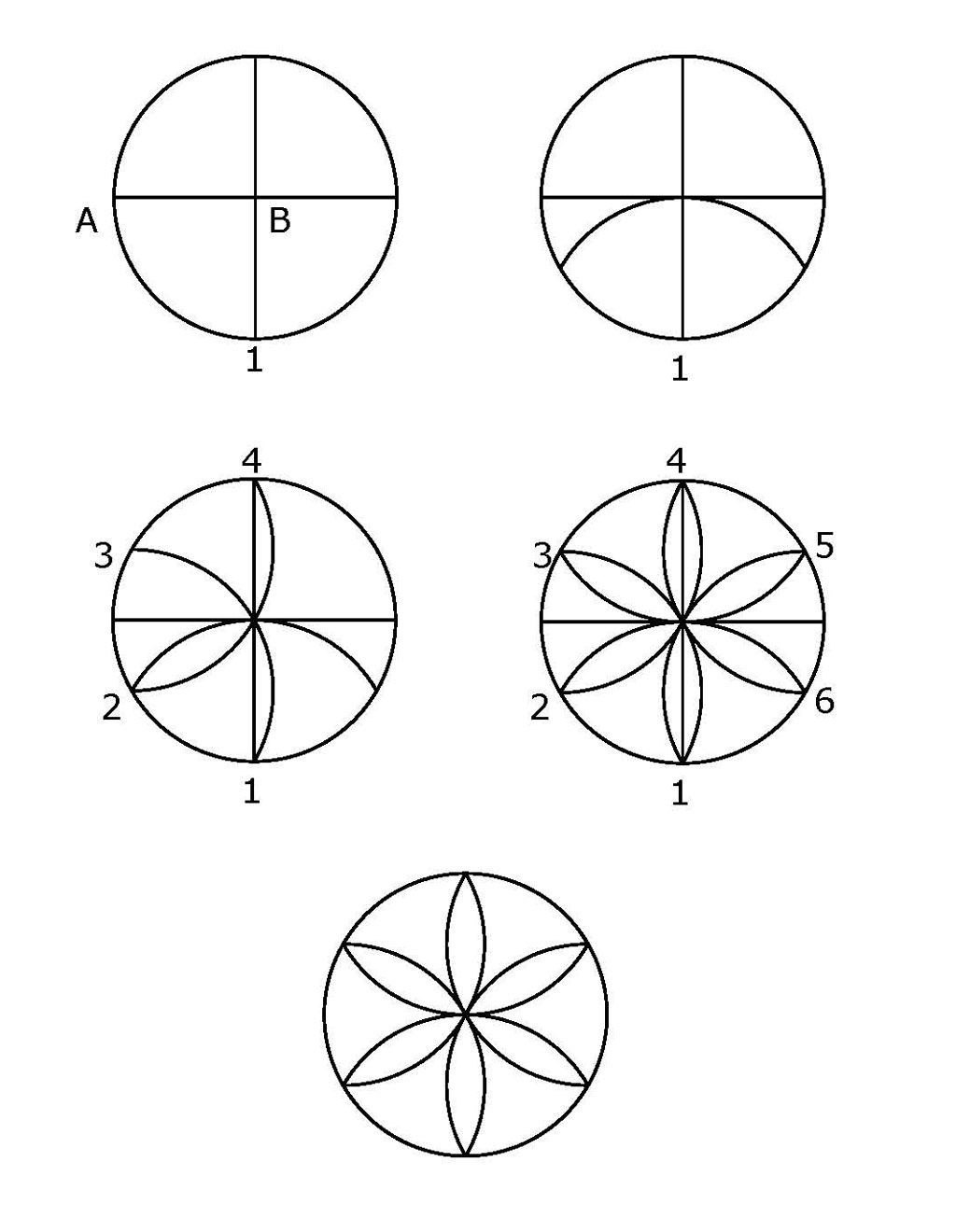
To draw the Euclidean six point geometry start with radius line AB on two perpendicular lines. Set your compass at B and draw the circle with radius AB. Next set your compass at point 1 and using the same radius AB swing the compass to draw the first arc that touches the sides of the circle.
Next set your compass at point #2 where the first arc touches the circle and swing another arc. Procede around the circle setting your compass at the intersection of the arc and circle to draw the rest of the arcs.
The six point geometry can also be call six rose petals, seed of life,
timber framing daisy wheel, Dutch Hexagram, thunder marks, hex rose
petal or the basis for the Star of David or that King Solomon’s
seal is based on six point geometry. The Vesica Piscis is also derived
from Euclid's Elements Book 1 Prop 1. The six petal flower design may
also be a signature, left behind during the passage of an apprentice
geometer or apprentice mason, one who knows the road to Euclid. When
you see the Euclidean six point geometric drawing on the Knights Templar
tombstone at St Magnus cathedral in Kirkwall, is it a six petal flower
design, daisy wheel or a religious hex symbol, or the seed of life symbol
or just six point geometric construction?
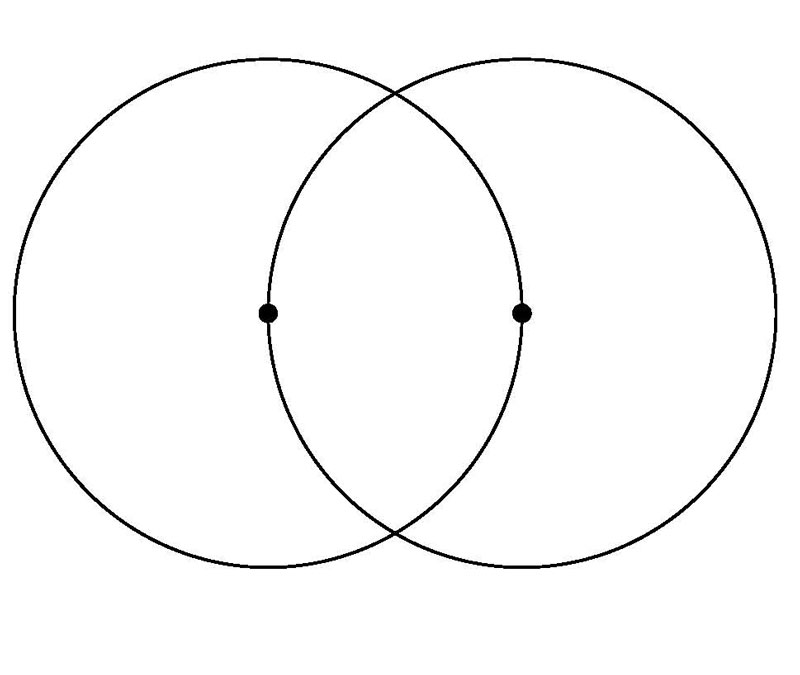
Vesica Piscis developed from Euclid's Elements Book 1 Prop 1.
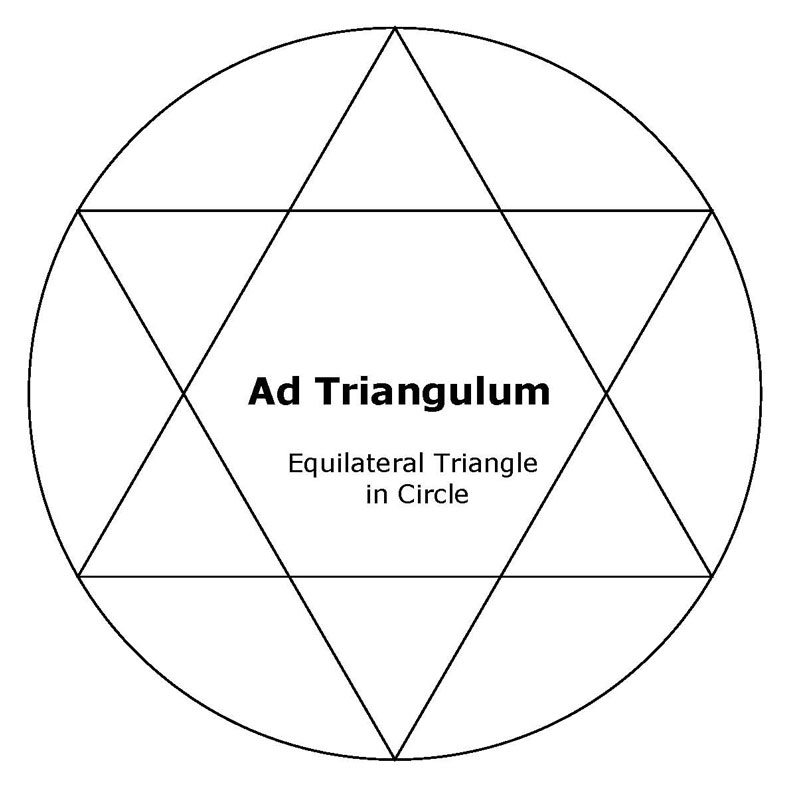
Ad Triangulum rotated equilateral triangles from six point geometry
If I get a chance to talk to French carpenters, who belongs to the
French compagnons carpenter guild system, I can say yes, I’ve
read-looked at one of the first book(in French) on carpentry by Philibert
De l'Orme, (1515 or 1576) LE TROISIEME LIVRE DE L’ARCHITECTURE
. Philibert De l'Orme discusses the geometry of Euclid, Archimedes and
Vitruvius. By studying De Architectura by Vitruvius, known today as
“The Ten Books on Architecture”, a treatise written in Latin
and Greek on architecture, Philibert De l'Orme uses symmetry and proportion
that was based on Ad Triangulum (Equilateral, Hexagonal base) and Ad
Quadratum (Rotated Squares, Octagonal based). Philibert De l'Orme also
discusses masonic projection (stereotomy) and his new invention, vault stick framing. Up until 1515, most
roofs were timber framed.
Ad Triangulum (triangle within the circle)
Ad Triangulum (hexagonal base)
Ad Triangulum (√3 base)
Ad Triangulum (three point geometry)
Ad Triangulum (six point geometry)
Ad Quadratum (square within the circle)
Ad Quadratum (octagonal based)
Ad Quadratum (√2 based)
Ad Quadratum (four point geometry)
Ad Quadratum (eight point geometry)
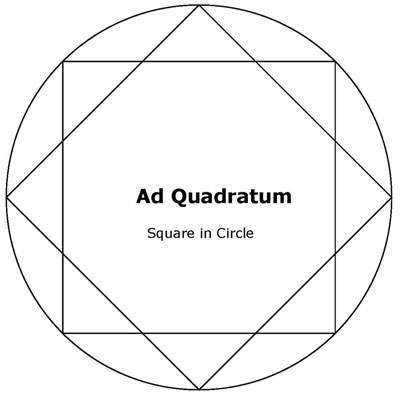
Ad Quadratum rotated squares from 4 point geometry
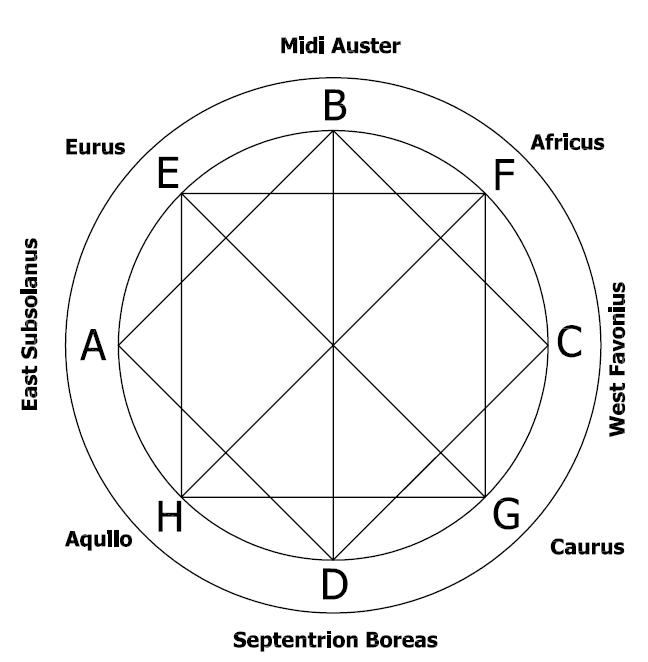
Philibert De l'Orme layouts the 8 wind directions for the orientation of a building based on Ad Quadratum.
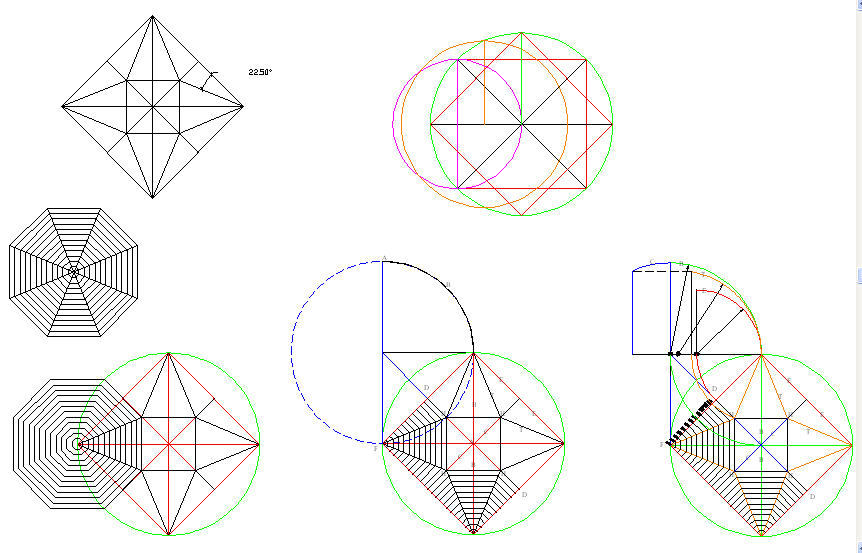
Philibert De l'Orme layouts the spherical cross vault based on Ad Quadratum.
Philibert De l'Orme was the inventor of the first speed square based on the Equilateral Triangle of Ad Triangulum.
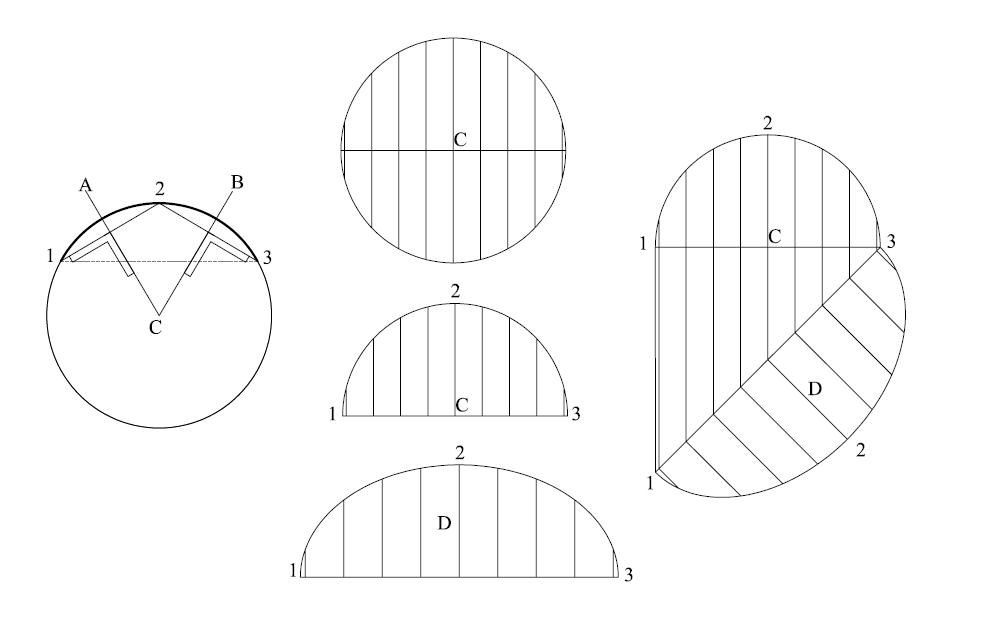
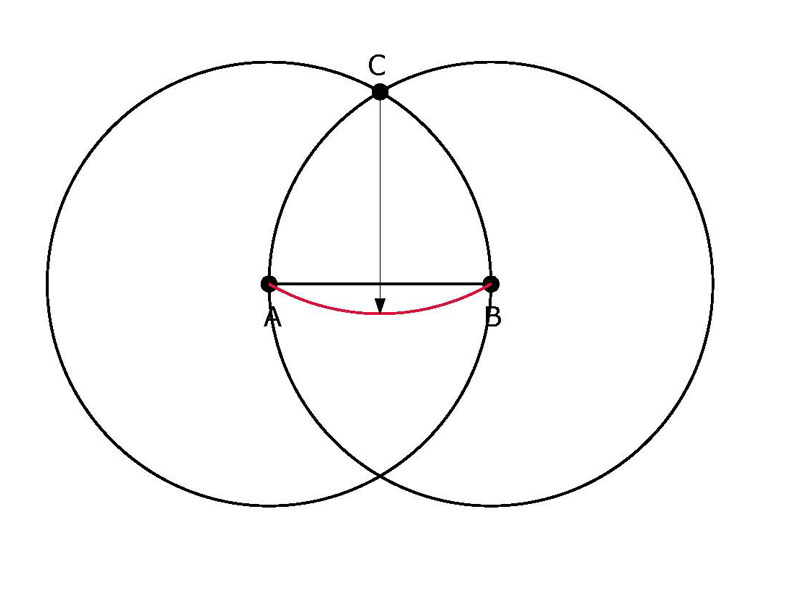
Philibert De l'Orme explains how to plot the points
of a lengthened arch (ellipse) from the 3 lost points of the arch.
Points A & B are the mid points of the chords and the point C is the
center of the circle located by the perpendiculars of the chords.
By suggesting that the 3 points were lost, Philibert De l'Orme is
saying that the builders he came in contact with had forgotten their
geometry. By calling the arch lengthened instead of an ellipse, it
shows that in the early 16th century (1515) no one had a clear understanding
of the mathematical properties of an ellipse. Leonardo da Vinci, Albrecht
Dürer, Hernán Ruiz and Mathurin Jousse also draw the ellipse
with ordinates but call it a lengthened arch [SANTIAGO HUERTA 2009].
However, Francois Derand in 1643 clearly shows a trammel for an ellipse
in his drawings. Another interesting description, by Philibert De
l'Orme, for developing the lengthened arch(Cherche rallongée)
is the use of "dropping perpendiculars" or "crawling lines". So I
don't think we'll find the use of the word "ordinates" in medieval
construction, even thou they developed their drawings using what we
call ordinates. Also, Philibert De l'Orme does not call it a new invention.
So the medieval builders must have known how to drop perpendiculars
and crawling lines to develop the lengthened arch.
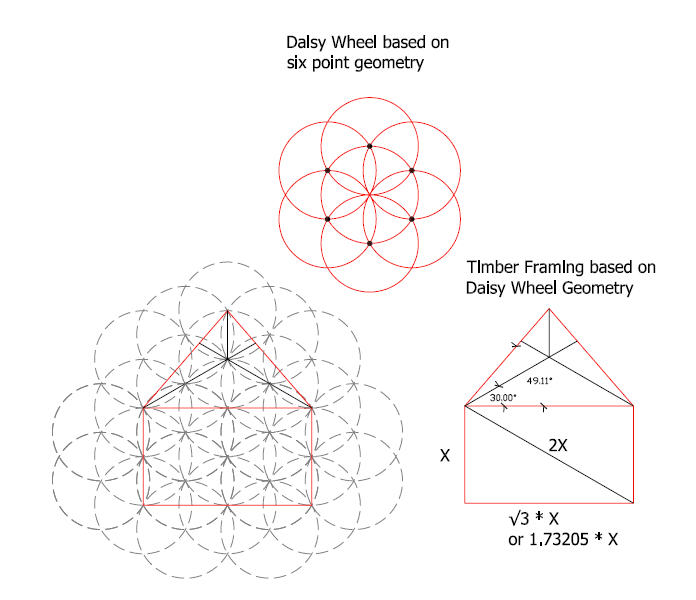
Daisy wheel used by medieval timber framing carpenters.
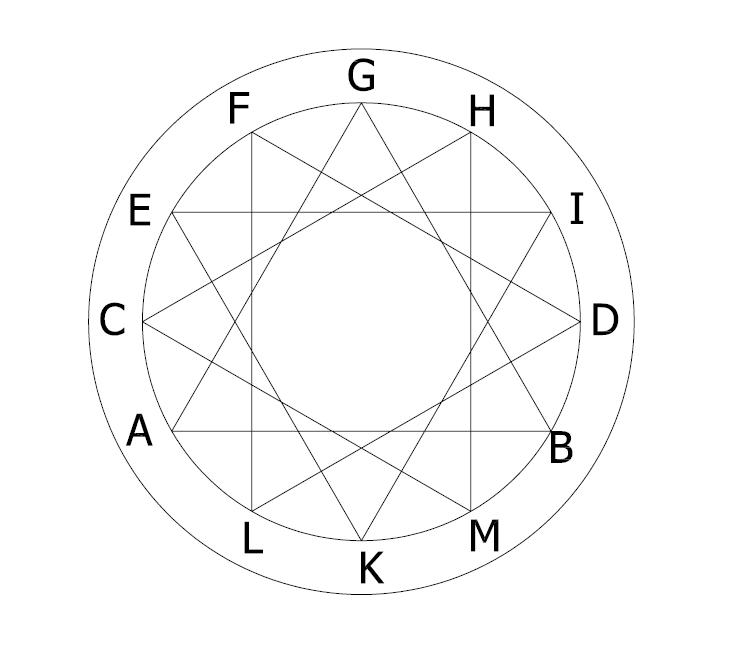
Vitruvius Roman Theater based Rotated Equilateral Triangles Ad Triangulum Geometry
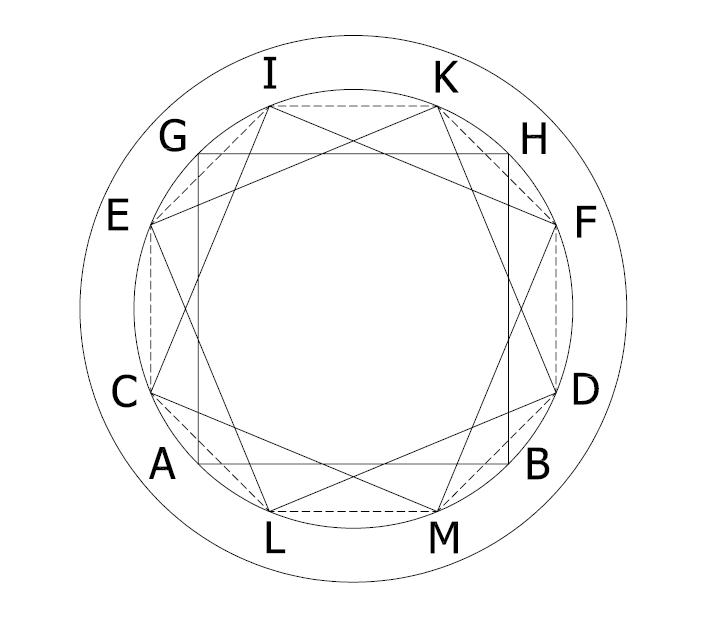
Vitruvius Greek Theater based on Rotated Squares Ad Quadratum Geometry
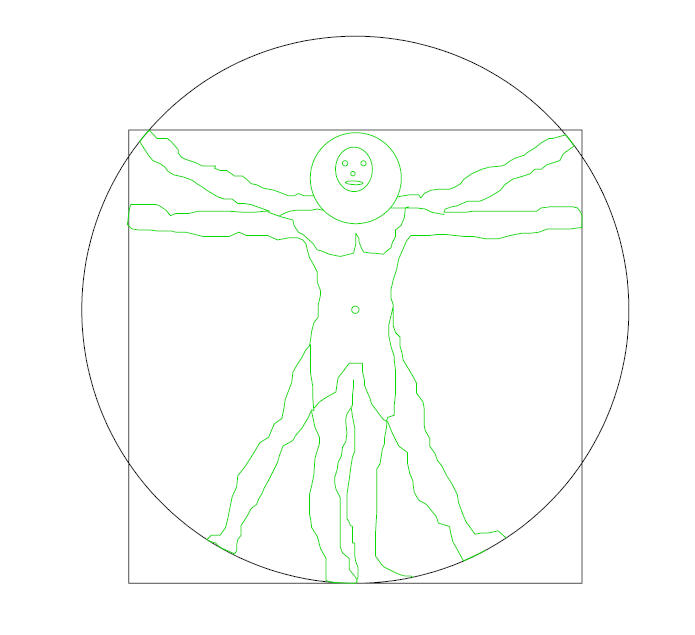
Vitruvian Man -- Little Green Men with Correct Porportions
Symmetry arises from proportion according to Vitruvian principles (70 BC).
So when you see a picture of the Vitruvian man by Leonardo Da Vinci (1451),
you know he based his drawing on Vitruvius, Book III, Chap. 1, on the circle
and square of Ad Quadratum. A square (homo ad quadratum), that is placed in
a circle (homo ad circulum). "Without symmetry and proportion there can
be no principles in the design of any temple; that is, if there is no precise
relation between its members, as in the case of those of a well shaped man."
Should the elevation of our houses have the proportions of a well shaped man
or should they be based on the golden ratio? Or Ad Triangulum Geometry? Can
we say that our house is based on Ad Quadratum Geometry if our house is square
or has octagonal geometry?
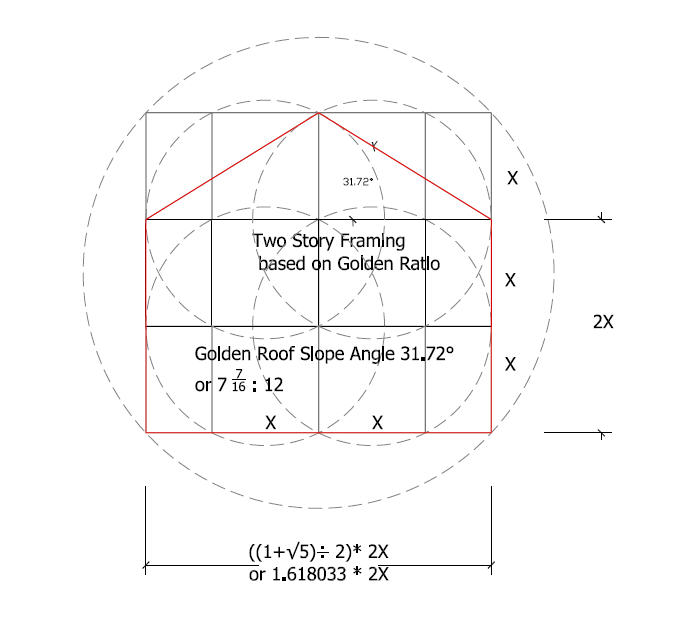
Golden Ratio Framing
Empirical geometry, information gained by means of observation, experience,
or experiment, used by masons and carpenters over the last 2000 years
is the root of applied geometry, namely the branch of geometry that
we call descriptive geometry today. Give a medieval mason or carpenter
a compass and the techniques that they used to draw out curved complex
cuts are called stereotomy. Descriptive Geometry is the theoretical
side of stereotomy. Is stereotomy based on the eleventh and twelfth
books of the Elements of Euclid? Or was stereotomy (masonic projection)
just a building technique by the masons and carpenters ?
The method of Ad Quadratum that is described by Roriczer in 1451 where he
takes a square and draws a diagonal square inside and in a series of
further steps gives the technique for "elevating" a cathedral pinnacle.
This general Ad Quadratum technique was used to produce other structures
including the cross-sections of buildings. Another medieval technique
of taking the floor plan to the elevation is based on the equilateral
triangle (Ad Triangulum). The first modern exercise in descriptive geometry
wasn't done until 1471 by German painter Albrecht Dürer. Albrecht Dürer
called the descriptive geometry of the ellipse from a conic section,
oval, or the egg line shape. So did the medieval carpenters draw ovals
instead of plotting out the ellipse with ordinates? There have also
been Egyptian cave drawings of the geometry to draw out ovals.
The difference between an ellipse and oval is so small that no one can really tell the difference between an ellipse and oval without measuring the oval.
Before the 16th century, builders only had extremely simple construction
geometry techniques. Villard de Honnecourt’s sketches in 1250
showed crude geometric forms of Euclidean geometry and were-are supposedly
the basis of freemason’s secret [Marie-Thérèse Zenner
2003]. It wasn’t until Gaspard Monge, wrote about "Descriptive
Geometry, or the Art & Science of Masonic Symbolism”, in 1776
the secret word was completely revealed.While the Romanesque builders
liked the symbolism of numbers that referred directly to the biblical
message and its interpretation, medieval masons and carpenters revered
above all, the geometry of Euclid from compass and straight edge.
Francois Derand (1588 -1644) published LES LIVRES D’ARCHITECTURE,
after Philibert De l'Orme, (1515 or 1576) LE TROISIEME LIVRE DE L’ARCHITECTURE
. Francois Derand, “The architecture of arches” could be
directly related to the descriptive geometry we use today to draw out
roof framing kernels, ellipses or groin vaults using ordinates.The secrets
of the professionnel builders, des maçons. Andrea Palladio, a
French architect also stuied Vitruvius and used the ellipse in his designs.
Some of Andrea Palladio drawings are egg shaped, while others are true
ellipses. It's hard to tell if Andrea Palladio had any real influnce
over the construction techniques of the Medieval - Renaissance builders.
Two other French architects/ mathematicians who might have influnced
the construction techniques of the Medieval - Renaissance builders are
Gérard Desargues and Amédée-François Frézier.
Any of these French architects/mathematicians could have been the basis
of the “British System of Projection”, by Peter Nicholson
in 1832 who could be considered the father of American roof framing
geometry. However, the French compagnon carpenter guild system might
argue that the roof framing geometry we use today is based off of the
book by Mathurin Jousse (1607–1692 French) or other books that
the French aren’t sharing. Louis-Mazerolle's (1889) Traite Theorique
Et Pratique De Charpente and Art Du Trait Pratique De Charpente by Emile
Delataille (1890) are good examples of stereotomic development at its
peak by French carpenters. Without being able to read French or German,
I’m only speculating that the stereotomic drawings of Francois
Derand are more precise than Philibert De l'Orme drawings, thus easier
to develop other construction geometric drawings from that were the
basis of our roof framing geometry. [updated] "Traict Five Orders
of Architecture" translated from Palladio by Pierre Dumb in 1645
has a lot better geometric roof framing drawings. It also has a Gambrel
Roof drawing. The Dutch published a counterfiet copy of the book in
1646, it looks like the Dutch Gambrel Roof is a Counterfeit French Mansart
Roof in more ways than one.

Orthographic projection & Stereotomic projection
Marcus Vitruvius Pollio, in De Architectura (80 BC), Book I, writes about orthography
and scenography, (orthographic projection and stereotomy projection). Stereotomy
relies on the use of horizontal and vertical projections in determining in two
dimensions the precise configuration of the 3 dimensional complex parts of a
building.
In the 10th century Persian mathematician Abul Wafa al-Buzjani at Baghdad
wrote the treatise "On Those Parts of Geometry Needed by Craftsmen".
Abul Wafa al-Buzjani writes about six point geometry and other types
of geometry needed by craftsmen. You can see some of this geometry each
time you step on your Persian rug and count the 3, 4, 5, 6, 7, 8, 10,
12, 16 or 20 point geometric shapes in the rug. Islamic geometry shows
the influence that Euclid, Vitruvius, Archimedes had on Islamic mathematics
after the late 8th century translation of Euclid's Elements into Arabic
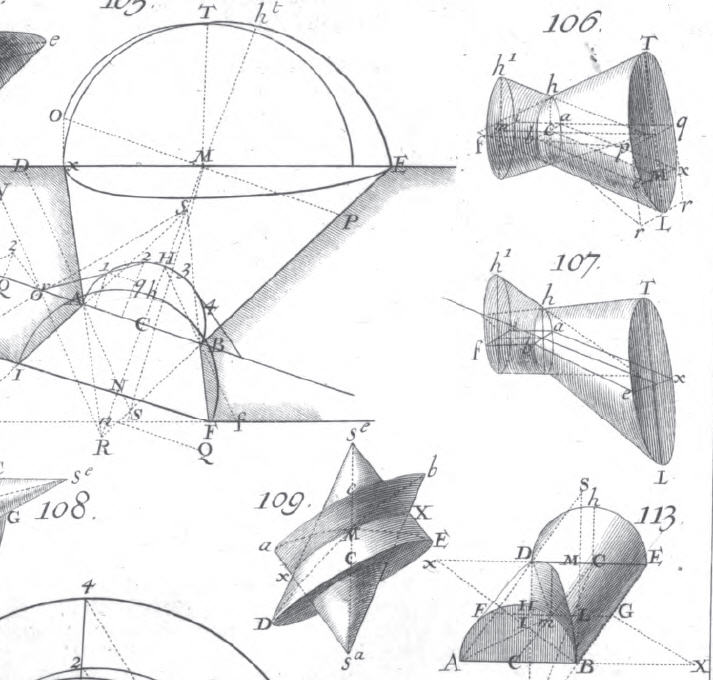
in Baghdad. Archimedes and Apollonius of Perga books on Conics, who
named the conic section, ellipse, parabolas, hyperbolas , were also
translated from Greek to Arabic and may be the reason for the medieval
builders using conic and spherical geometry for their vaults instead
of the Romanesque barrel vaults or groin vaults. Was medieval French
stereotomy based on the orthography and scenography that Vitruvius describes,
or was it developed-influenced by the books from Baghdad?
Why is the colonial crown molding spring angle at 38° - 52°. Is it
based on the golden ratio of phi? (1 + √5)/2 = 1.618033989. The arctan (√phi)
= 51.83°. The inverse slope of 90° - 51.83° = 38.17°
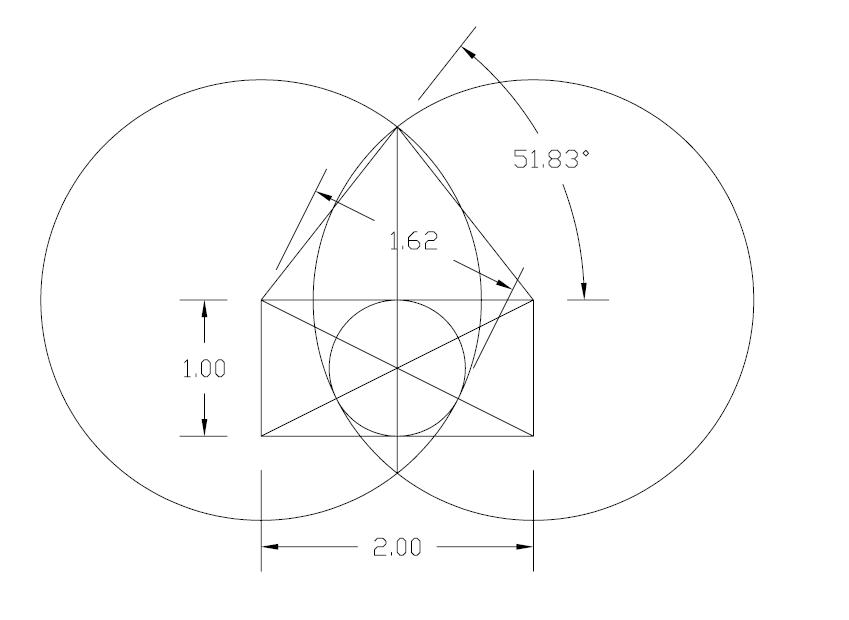
Circle inscribed in a 1:2 rectangle produces the golden ratio of phi and
the 51.83° slope of the pyramid
Egyptian pyramids base (b)= 1, √phi = height(h), phi = apothem(a), slope angle
= arctan(√phi ) = 51.83° . The Romans kept the golden ratio as the uniform
proportion in their construction (major axis/minor axis of the ellipse), width
and height of steps, (tread & riser) width and height of the rows around
the Coliseum of Rome.
Formula for a golden ratio ellipse
Minor axis = X
Major axis = X * 1.618033989
Formula for a golden ratio stairs
Stair Riser = X
Stair Tread = X * 1.618033989
(7” riser = 7 * 1.618033989) = 11 5/16” tread
Formula for a golden ratio Roof slope
Rafter Run = X
Rafter Slope = X * (1.618033989 – 1)
(12” run = 12 * (1.618033989 – 1) = 7.416= 7 7/16 = 31.72°)
Or is the colonial crown molding spring angle based on the umbra recta shadow?
The Greeks and Romans developed sundials based on the length of the shadow
cast by a stick-gnomon. The umbra recta simulates the shadow cast on the horizontal
plane by a vertical gnomon when the Sun's ray is inclined between 0° and
45°. The umbra versa simulates the shadow cast on the vertical plane by
a horizontal gnomon when the Sun's ray is inclined between 45° and 90°.
When the Sun’s ray is inclined by 45°, the two shadows are equal (umbra
media).
Vitruvius - Ptolemy Alalemma-Sundial from 12 point geometry and orthographic projection

Vitruvius the Alalemma Sundial and Its Applications Book 8, Chapter 7
The ellipse, and its centre, is the point at which all Elliptical Geometry
begins.
By plotting abscissas and ordinates of the sun's shadow, you can drive the
chariot of the sun's arc south of the equator to see the chariot of light
at winter solstice.
After developing the drawing from Vitruvius “The Alalemma Sundial
and Its Applications” Book 8, Chapter 7, I’m amazed at the
geometry that was developed over 2000 years ago. The Elliptic “Alalemma
Sundial” would have been developed using ordinates. So the use
of ordinates would have been general knowledge to the medieval builders
to build an elliptic sundial who wanted to know when to stop work for
the day to head to the ale taverns to have strong beer after drinking
weak beer for breakfast and lunch along with their stale horse bread.
Conclusion
It could take years to read and analize all of the books written on
vaulting. Robert Willis wrote the book " On the Construction of
Vaults of the Middle Ages" where he discusses Gothic vaulting techniques
and the stereotomy by Philibert De l'Orme, Francois Derand, De la Rue,
Mathurin Jousse, Amédée-François Frézier
and others. Willis said the Gothic rib vaulting used only circluar arcs
and no elliptical vault ribs were used. An easy way for the medieval
builders not to know anything about drawing out an ellipse.
Philibert De l'Orme and Abul Wafa al-Buzjani both criticized the masons
and carpenters for sloppy construction due to a poor understanding of
geometry. Probably only 10% of the medieval masons and carpenters really
knew their geometry, which is no different than today. I’m pretty
sure if we ask the carpenters of today to plot an ellipse using the
abscissas(X) and ordinate(Y) of an ellipse, you’ll get a blank
stare of fright. Even thou it’s called “the trammel of Archimedes”,
there’s no documented evidence of it being used before the 16th
century and it would have been tough to build a trammel for a 32’
or 48’ major axis. The use of a rope or string for drawing an
ellipse was first brought to light in the 6th century by Anthemius of
Tralles , a Greek professor of Geometry in Constantinople, where they
built 336 groin vaults underground in Constantinople for water storeage.
However, there is never any real documentation of the medieval builders
using the string method. With a lot of the medieval vaults based on
conic and spherical geometry the rope or string or trammel method would
have been useless on parabolas, hyperbolas or double curves surfaces
from the intersection of a cone and sphere. More questions arise than
answers, but at least I now know, according Vitruvius, that towers should
be either round or polygonal, never square. And that the distance between
each tower should not exceed an arrow's flight.
A cubit is a forearm, from the elbow to the tip of the fingers.
|