Medieval vaulting geometry research, links, notes and keywords

Treatise On Those Parts of Geometry Needed by Craftsmen PDF files

A lesson in Applied Geometry and Euclidean Geometry

String Theory on Medieval Masons and Carpenters drawing an Ellipse

  π

Stereotomy: The Alchemy Of Solids
Taking something ordinary and turning it into something extraordinary
Rene Salas
A Tour de France in the study of l'Art du Trait & the Compagnon. These historic craft guilds have developed and maintained a system of craft that have produced many world renown architectural treasures. Who are they, and what could their impact be on todays building culture?

  π

Nexus Network Journal 9,2: Architecture and Mathematics
Oval Domes: History, Geometry and Mechanics Santiago Huerta
Oval Domes: History, Geometry and Mechanics Santiago Huerta

Sloan's constructive architecture : a guide to the practical builder and mechanic (1859)
4 rectangles of crown moulding design-layout page 232
"In which is contained a series of designs for domes, roofs and spires, with a number of plates showing the interior construction and finish of bays, window shutters, sliding doors, etc., designed expressly for the joiner's use; choice examples of the five orders of architecture, selected from the most celebrated specimens of antiquity, with the figured dimensions of their height, projection and profile, and their division into parts; to which is added a number of useful geometrical problems, examples of groins, centering for arches, diagrams of stair lines, with architraves, door moldings, etc.; the whole being illustrated by sixty-six carefully prepared plates, accompanied by explanatory text and general essays, to which is appended a copious glossary"--T.p
Sloan's constructive architecture : a guide to the practical builder and mechanic

Encyclopedia of architecture : a dictionary of the science and practice of architecture, building, Carpentry, etc., from the earliest ages to the present time, forming a comprehensive work of reference for the use of architects, builders, carpenters, masons, engineers, students, professional men, and amateurs ([185-?])
Volume 2
Peter Nicholson ( 1765-1844) talking about Vitruvius
Peter Nicholson talking about Vitruvius
Peter Nicholson talking about Brunelleschi
Peter Nicholson talking about sima recta crown moulding design
Peter Nicholson talking about panormara projection
Peter Nicholson talking about panormara projection
Peter Nicholson talking about stereotomy spherical Triangles spherical Trigonometry
V-1 Peter Nicholson talking about Bracketing
V-1 Peter Nicholson talking about Double Curveture Arches
V-1 Peter Nicholson talking about Conic Sections
V-1 Peter Nicholson talking about Cylinders
V-1 Peter Nicholson talking about Domes
V-1 Peter Nicholson talking about Ovals and Ellipses
V-1 Peter Nicholson talking about Hip Roof Geometry

Solid Geometry for Builders .. Hoppers Practical geometry for builders and architects 1921

Cyclopedia Of Architecture, Carpentry, And Building Vol7-10
Cyclopedia Of Architecture, Carpentry, And Building Vol7-10
The encyclopædia britannica Vaulting 1911

Mouldings of the Tudor period : a portfolio of full size sections-- Small, Tunstall
The Standard moulding book 1920
Guide for drawing the acanthus, and every description of ornamental foliage

Sloan's constructive architecture : a guide to the practical builder and mechanic. In which is contained a series of designs for domes, roofs and spires, with a number of plates showing the interior construction and finish of bays, window shutters, sliding doors, etc., designed expressly for the joiners use; choice examples of the five orders of architecture, selected fromthe most celebrated specimens of antiquity, with the figured dimensions of their height, projection and profile, and their division into parts,; to which is added a number of useful geometrical problems, examples of groins, centering for arches, diagrams of stair lines, with architraves, door mouldings, etc., the whole being accompanied by explanatory text and general essays, to which is appended a copious glossay
Sloan's constructive architecture

Roof framing made easy: a practical and easily comprehended system, adapted ... By Owen Bernard Maginnis
Roof framing made easy 1896 Maginnis, Owen B. (Owen Bernard), b.

Egypt, Greece, Roman, France, Islamic

http://www.en.charpentiers.culture.fr/treesintohouses/thecarpentersart/specialistliterature

Technical knowledge about wood and framing appear in specialist literature that was particularly abundant between the 16th and 19th centuries.

https://www-docs.tu-cottbus.de/bautechnikgeschichte/public/openaccess/negre_oa.pdf

Some Considerations on Traité de L’Art de Bâtir by Rondelet and the
Technical Literature of his Time

The contemporary world of building is dominated by standardization and mechanization that are transforming builders into mere labourers devoid of any creative thinking.

http://www.google.com/url?sa=t&source=web&cd=1&ved=0CBYQFjAA&url=http%3A%2F%2Fwww.unesco.org%2Fculture%2Fich%2Fdoc%2Fsrc%2F00251-Nomination_form.doc&rct=j&q=Nicolas%20Fourneau%20french%20carpenter&ei=LZjmTND8No7GsAO-2biwCw&usg=AFQjCNHKvkcTVLoEnnlV_27t_esxyU9JKg&sig2=S2N7zqGj2vFUpfbCp6slew&cad=rjt

The scribe tradition in French timber framing, or the “trait de charpente” as the carpenters call it, makes it possible to design complex wooden buildings in three dimensions.

The symbolic aspects of instruction in the French scribe method are revealed in the context of the Compagnonnage only in a confidential manner during joining and induction ceremonies. These very particular circumstances are not open to outsiders, nor are they communicated to the outside world in any way. However, the general principles of this instruction, the universal aspects of which are affirmed by the Companions themselves, can be disseminated without restraint. The technical and historic aspects of scribing, the production of masterworks and masterpieces at the end of apprenticeships may be referred to normally, taking into account, of course, the great complexity of some productions.

LaHire, Philippe de, La gnomonique ou methodes universelles, pour tracer des horloges solaires ou cadrans sur toutes sortes de surfaces , 1698

Gabriel-Philippe de LaHire (1677-1719), in mathematics

Mathurin Jousse's work, published in 1627, reprinted and supplemented by Gabriel Philippe de La Hire in 1702, illustrating the implementation of various framing attic, timber framed or stairs, is the first expression.
http://architectura.cesr.univ-tours.fr/Traite/Notice/CESR_IHA615.asp

http://echo.mpiwg-berlin.mpg.de/ECHOdocuView?pn=336&url=%2Fmpiwg%2Fonline%2Fpermanent%2Flibrary%2FUSVW0U1V%2Fpageimg&start=331&viewMode=images&mode=imagepath

http://echo.mpiwg-berlin.mpg.de/ECHOdocuView?pn=340&url=%2Fmpiwg%2Fonline%2Fpermanent%2Flibrary%2FUSVW0U1V%2Fpageimg&start=331&viewMode=images&mode=imagepath

 

Stereotomy a multifaceted technique
Descriptive geometry, belongs to the history of techniques through its origins, While stereotomy, together with carpentry, provides
one of the richest examp]es of the uses of applied geometry, it is also at the root of a branch of erudite geometry, namely descriptive geometry.
Before the 18th century, builders only had extremely simple, purely geometric and (at best) empirical «rules» at their disposal to size the building s under construction. One of the most famous rules is the «Leonardo rule», which says the arch will not break if the chord of the
outer arc does not touch the inner arc.

Descriptive Geometry == «theoretical stereotomy», detached from its original function as a technique of stone cutting

Sand Geometry
Light Geometry
Egyptian Geometry
Greek Geometry
Roman Geometry
Arabic/Islamic Geometry
Persian Geometry
Pythagoras Geometry
Euclidean Geometry
Vitruvian Geometry
Archimedes Geometry
Apollonios Geometry
Sacred Geometry
Vesica Piscis Geometry
Ad Triangulum Geometry
√3 Geometry
Ad Quadratum Geometry
√2 Geometry
Euclid Elements
Euclidean postulates
Vitrúvio
Vitruvius
Vitruvian principles
Symmetry Arises from Proportion
A cubit is a forearm, from the elbow to the tip of the fingers.

analemmas
dos princípios vitruvianos
Ad Triangulum
Ad Quadratum
Ad Quadratum, Ad Triangulum and The Sacred Cut
The Vesica Piscis and Squaring of the Circle

Ad Triangulum ( triangle within the circle)
Ad Triangulum (hexagonal base)
Ad Triangulum (√3 base)
Ad Triangulum (three point geometry)
Ad Triangulum (six point geometry)
Ad Triangulum (human consciousness)
Ad Triangulum (Heaven)

Ad Quadratum (square within the circle)
Ad Quadratum (octagonal based)
Ad Quadratum (√ 2 based)
Ad Quadratum (four point geometry)
Ad Quadratum (eight point geometry)
Ad Quadratum (earth geometry)
Ad Quadratum (physical world)

Ad Quadratum -- Height =( width * √ 2) / 2
Ad Triangulum -- Height = width * (√3 / 2)

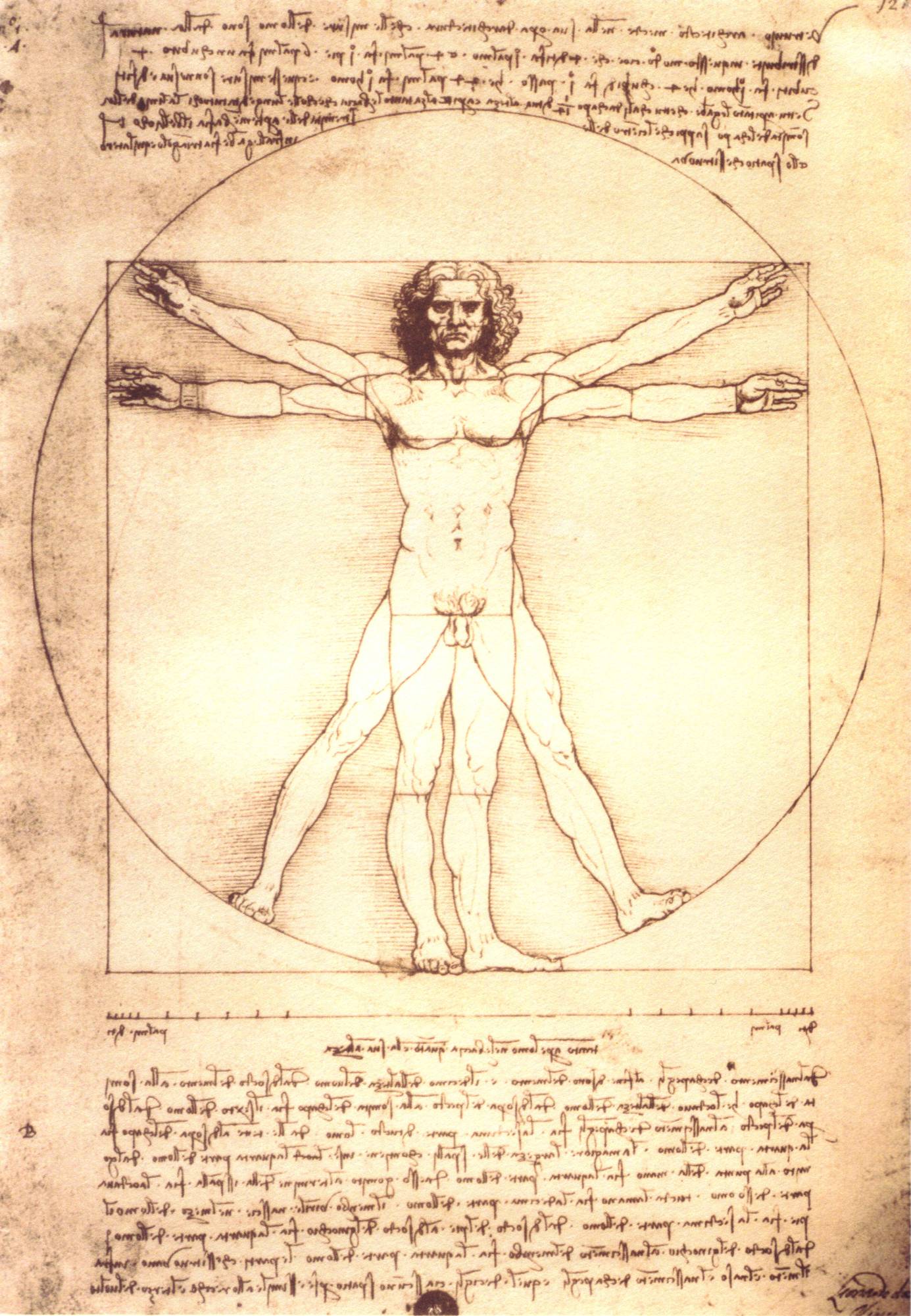
Vitruvius wrote that if a figure of a correctly proportioned human body were placed within a square (homo ad quadratum), which in turn was placed in a circle (homo ad circulum) in such a way that the corners of the square were just touching the arc of the circle, then the precise centre of both the circle and the square would be the human figure's navel (umbilicus ad circulum et ad quadratum). <\p>
2* π * height = perimeter
√2 = 1.414

Golden Ratio phi = (√5 + 1) ÷ 2 ) = 1.6180339887
Euclid -- extreme and mean ratio
Luca Pacioli --"divine proportion" in Divina Proportione
Egyptian pyramids base (b)= 1, √phi = height(h), phi = apothem(a), slope angle = arctan(√phi ) = 51.83°
1:1.414
12 times 1.414 is 16.97”
"Without symmetry and proportion there can be no principles in the design of any temple; that is, if there is no precise relation between its members, as in the case of those of a well shaped man."
Vitruvius, Book III, Chap. 1
Six petalled rose
Sun-rosette
Daisy wheel
Flower of Life
Seed of Life
Morning Star
Dutch Hexagram
Vesica Piscis
Thunder Bolt Marks
Tripod of Life
Ancient Egyptian Seal of Solomon
6-pointed star
SIX TRIANGLES...is the Egyptian hieroglyphic for the ...Land of the Spirits.
6-pointed star was the first sign or hieroglyphic of Amsu
STAR OF YOUR GOD
Light Geometry
Romania geometry thunder rosette
carpenter geometry thunder rosette
"Halloween...emanates from the 14th century... when the Druids would knock on the doors of the castles demanding the young maiden or princess for their sacrifices. If they were not given the maiden, they would paint a HEXAGRAM on the door to tell...that all should die in that household."
8 pointed star , star of the dawn or MORNING STAR'
The Menorah, not the Hexagram is the true symbol of God's covenent with the Jewish people.

Many Jews and Christians have been deceived by Jewish Kabbalists who would have them believe that the six-pointed star is a Jewish symbol. Nothing could be further from the truth. It is not a Jewish symbol, but an occult symbol. The six-pointed star is a hexagram – a curse mark – no matter what name it may have: the Star of David, Solomon’s Seal, Double Triangle, Shield of David, etc. When the occult practitioner puts a curse on someone, he uses the hexagram (a “Hex!”)

“The Universal Jewish Encyclopedia declares that the SIX-POINTED STAR…according to the Rosicrucians…was known to the ancient Egyptians.” “SIX TRIANGLES…is the Egyptian hieroglyphic for the …Land of the Spirits.” “Ancient Egyptian Seal of Solomon” “In the Astro-Mythology of the Egyptians, we find belief in the first man-god (Horus I) …and his death and resurrection as Amsu” “This (6-pointed star) was the first sign or hieroglyphic of Amsu” “Amsu – the risen Horus – was the first man-god risen in spiritual form.”

Geometry is the greek word for earth measure, using angles with predictably moving stars to measure the earth in ancient times, as the Greek unit of length, the stade, is 600 greek feet (of 12.16 modern inches).

Medieval baptismal font
Gothic architecture
Gothic history
Gothic Mason’s Marks
Voutes
Vault
Ribbed Cross vault diagonals
Ellipse
Oval
intersection horizontal vertical cylinder
Cone
Cylinder
Sphere
Platonic Solids
Intrados
Cylindroid
Spheroid
Spherical elliptic geometry
De Charpentier
Carpenter
Helicoidallywarped = skewed arch
conoids, hyperboloid arches
Trumpet arch
Warped surfaces arches of double curvature.
A obra, intitulada On the Ordination of Pinacles, Röriczer
Canônico
Canonical
Speculative Masons
maçons especulativos

chronological list of some of the most important mathematicians in history
The Story of Mathematics

Pythagoras of Samos (c. 570-c. 495 BC)
Plato(c. 428/427 BC– 348/347 BC)
Archytas of Tarentumwas(428–347 BC) Archytas Curve--determining a certain point as the intersection of three surfaces of revolution, (1) a right cone, (2) a cylinder, (3) a tore
Euclid(300 BC)
Archimedes of Syracuse(c.287BC –c.212BC)
Apollonius of Perga[Pergaeus] (ca. 262 BC–ca. 190 BC)
Claudius Ptolemy (2nd C. C.E.)
The oldest known work on trigonometric tables is the Syntaxis Mathematica written by Ptolemy of Alexandria about 140 AD.

The Theorem of Ptolemy
According to the theorem of Ptolemy, if a quadrilateral is inscribed in a circle, the sum of the products of the two opposed sides is equal to the product of the multiplication of the diagonals.
According to the quadrilateral PQRS, we have the following formula.
PR x QS = PQ x RS + PS x QR.
The theorem of Ptolemy is as follows:
c2 (a) = 60 c2 (2 a) / 120 + c (180 – 2 a)

Marcus Vitruvius Pollio(c. 80–70BCE, c. 15 BCE)
Mathes Roriczeralso Matthäus Roritzer, Röriczer (1435-1495)
Piero dellaFrancesa(c.1415–92)
Fra Luca Bartolomeo de Pacioli(1446 - 1517)
Leonardo di ser Piero daVinci(1452 –  1519)
Albrecht Durer(1471–1528)
Diego de Siloé(c.1490–1563)
Philibert de L’Orme (1514–70)
François Derand(1588or1591–1644)
Mathurin Jousse(1607–before1692)master locksmith
Gérard Desargues(1591–1661) my favorite
Amédée-François Frézier(1682–1773)
Gaspard Monge(1746–1818)
Charles-François-Antoine (1780-1854)
Mahan, D. H. (Dennis Hart), 1802-1871
Robert Willis (1800-1875)1843 gothic vaulting
De Divina Proportione (1509)

Fra Luca Pacioli.

Leonardo da Vinci
Stereotomy
Stereography
Stereotomic
Stereotomique
Stereotomic treatises
Skewed arches,trompes
Stone cutting
Complex stereotomic cuts
Stereotomically complex cuts
Traite de stereotomie
Traite Descriptive Geometry
Stereotomic descriptive geometry

Traite de stereotomic descriptive geometry
Traite de stereotomy descriptive geometry
Companions of the Tour de France
Vault crossed with ribs
Pendentive
Cistercian monasteries
Euclid Conic sections
Canted elliptical arcs
elliptical half-cylinder
golden number is (1 + √5)/2 = 1.618033989
Great Pyramid rise at an angle of 51° 52'.
Vault descriptive geometry INTERSECTIONS OF CURVED SURFACES
Medieval building techniques
Valknut symbol
gotland churchs

Anahata chakra
Symbolizes the consciousness of love, empathy, selflessness and devotion. On the psychic level, this center of force inspires the human being to love, be compassionate, altruistic, devoted and to accept the things that happen in a divine way.

Square oven four, spandrel
Church
Cathedral
Spherical vault
Voussoirs
Freemasonry
Tectonic
Tekton
Orthographic projections
Mediaeval practical geometry
Plane Geometry
Centring
Centering
Trammel of Archimedes
An ellipsograph is a trammel of Archimedes intended to draw, cut, or machine ellipses, e.g. in wood or other sheet materials.
J. W. Downs: Practical Conic Sections: The Geometric Properties of Ellipses, Parabolas and Hyperbolas.
Frustum of a Cone
 Walk as children of light
Oculus(pluraloculi) is the Latin word foreye

Author (s) Jousse, Mathurin
Title The scene of the carpenter's art ...Title The secret architecture .
Address The Arrow, George Griveau, 1627
Location Paris, BENSBA Reserve SLE. 1250
Words matter Carpentry, Orders

Mathurin Jousse is best known for having written between 1627 and 1642, three treaties building devoted to the locksmith, carpentry and stereotomy, The faithful initiation of the locksmith art, theater art of carpentry and Secrecy architecture.

http://architectura.cesr.univ-tours.fr/traite/Notice/ENSBA_LES1250.asp

http://www.insitu.culture.fr/article.xsp?numero=1&id_article=flb001-857

 

Author (s) Derand, François
Title The architecture of arches ...
Address Paris, Sebastien Cramoisy, 1643
Location Besancon, City Library, 11598
Words matter Stereotomy, vaults

Derand Francis was born in Vic-sur-Seille in the diocese of Metz between 1588 and 1591.

http://architectura.cesr.univ-tours.fr/traite/Notice/B250566101_11598.asp

Author (s) Androuet Hoop, Jacques
Title Quinque and viginti arcuum exempla ...
Address Orleans, sn, 1549
Location Paris, Binh, 4 RES 1475
Words matter Arcs Entries

http://architectura.cesr.univ-tours.fr/traite/Notice/B250566101_11598.asp

 

Author (s) Dumb, Pierre
Title Traict five orders of architecture, which have seruy elders. Translated from Palladio Increased tidings of such device for the art of well built ...
Address Paris, Francois Langlois, 1645
Location Paris, BENSBA THE 646
Words matter Carpentry, Orders, Door Gambrel Roof

http://architectura.cesr.univ-tours.fr/traite/Notice/B250566101_11598.asp

Roof Truss within Arches

http://architectura.cesr.univ-tours.fr/traite/Images/LES646/ENSBA_LES646_247.jpg

The Dutch Gambrel is taken from this reprint by Palladio that the Dutch Stole

http://architectura.cesr.univ-tours.fr/traite/Images/LES646/ENSBA_LES646_258.jpg

François Mansart (13 January 1598 in Paris - 23 September 1666 in Paris) was born to a master carpenter

counterfeit French Mansart Roof --> Dutch Gambrel Roof

published in France 1645, counterfeit Palladio published in Amsterdam in 1646

http://architectura.cesr.univ-tours.fr/traite/Notice/ENSBA_LES646.asp?param=

This partial translation of Palladio, Book I, enjoyed a second printing two years later, in 1647, at Pierre Mariette. Three counterfeit Dutch successively published in Amsterdam in 1646, 1679 and 1682 attest to its success. In 1646 the book was translated into Dutch, and was also published in London in 1663 and continually reprinted. The fortunes of Palladio The Mute in northern Europe is likely due to its particularity: revised and corrected in the French style, this version was better suited to the Italian edition of practitioners whose ideas and techniques, climate forcing, were close.

 

Carpentry

L'Orme, Philibert (1514-1570)
New inventions for ... well built, Paris, Frédéric Morel, 1561.
New inventions for ... well built , Paris, and William Jerome Marnef Cavellat, 1576

Jousse, Mathurin
The art of theater carpenter enriched various figures ... , La Fleche, George Griveau, 1627.
The art of theater carpenter enriched various figures ... , La Fleche, George Griveau, 1650.
The scene of the carpenter's art, various figures ... enriched in La Fleche, Widow of George Griveau, 1659.
The art of theater carpenter enriched various figures , La Fleche, Widow of George Griveau, 1664.
The art of carpentry ... Fixed & increased ... By Mr. DLH .. , Paris, Moet Thomas, 1702.

Dumb, Pierre (1591-1669)
Basti way for all kinds of people , Paris, Melchior Tavernier, 1623
Manner of well built for all sorts of people , Paris, Francois Langlois, 1647
Manner of well built for all sorts of people ... ; Increase new ... bastimens, Paris, Jean du Can, 1663.
Treaty of Palladio
Traict five orders of architecture ... Translated from Palladio increased tidings inventions for the art of bastir by Sr. The Mute , Paris, Francois Langlois, 1645.

Stereotomy

Blondel, Francois (1618-1686)
Four problems
Resolution of the four main problems of architecture , Paris, Imprimerie Royale, 1673.

Derand, Francis (1588? -1644)
The architecture of arches, or the art features and cutting vaults ... , Paris, Sebastien Cramoisy, 1643.

Desargues, Girard
Practice relating to evidence, Mr Desargues Lyonnois, to cut stones in architecture ... , Paris, Pierre Deshayes, 1643.

L'Orme, Philibert (1514-1570)
The first volume of the architecture ... , Paris, Frédéric Morel, 1567.
The architecture ... , Paris, and William Jerome Marnef Cavellat, 1576.
The architecture ... , Paris, Guillaume Auvray, 1603.
... Full implementation architecture containing Unze Books, plus two ... , Paris, Regnault Chaudière II, 1626.
... Full implementation architecture containing Unze Books, plus two ... , Rouen, David Ferrand, 1648.

Jousse, Mathurin
The Secret ... architecture , La Fleche, George Griveau, 1642.

Perrault, Charles (1628-1703)
Parallel
Parallel of the Ancients and the Moderns, which looks into the arts and sciences. ... Dialogues , Paris, Jean-Baptiste Coignard, 1688 (Volume 1).

Antonio da Sangallo the Younger
http://www.all-art.org/history230-7-1.html
The Architectural Drawings of Antonio da Sangallo the Younger and His Circle
Volume 1 - Fortifications, Machines, and Festive Architecture

Hans Lencker Perspectiva

Squaring the Circle: Geometry in Art and Architecture
Calter, Paul A., Vermont Technical College

The six-petalled flower design may, therefore, be a kind of signature, left behind during the passage of an initiated geometer, that is, "one who knows the road to Egypt."
Villard de Honnecourt and Euclidean Geometry -- Marie-Thérèse Zenner

Master carpenters who coped with Greek revival styles during the 18th and early 19th centuries employed a variety of constructive methods to create the ornate curves these styles demanded. Handbooks like Asher Benjamin’s The American Builder’s Companion compiled these techniques for carpenters to reference.
Drawing Hour Lines with Elliptical Coordinates
The American builder's companion : or, A system of architecture, particularly adapted to the present style of building ; illustrated with seventy copperplate engravings (1827)

Sacred Stones project of the Abbey of New Clairvaux
http://www.sacredstones.org/
Sacred Stones Chapter House Construction, 2010
http://picasaweb.google.com/106628474194260084428/ChapterHouseConstruction2010#

Ad Quadratum, the Sacred Cut, & Roman Architecture
http://www.dartmouth.edu/~matc/math5.geometry/unit5/unit5.html

LES LIVRES D’ARCHITECTURE, Derand Francis, Stereotomy, vaults, Trammel for ellipse

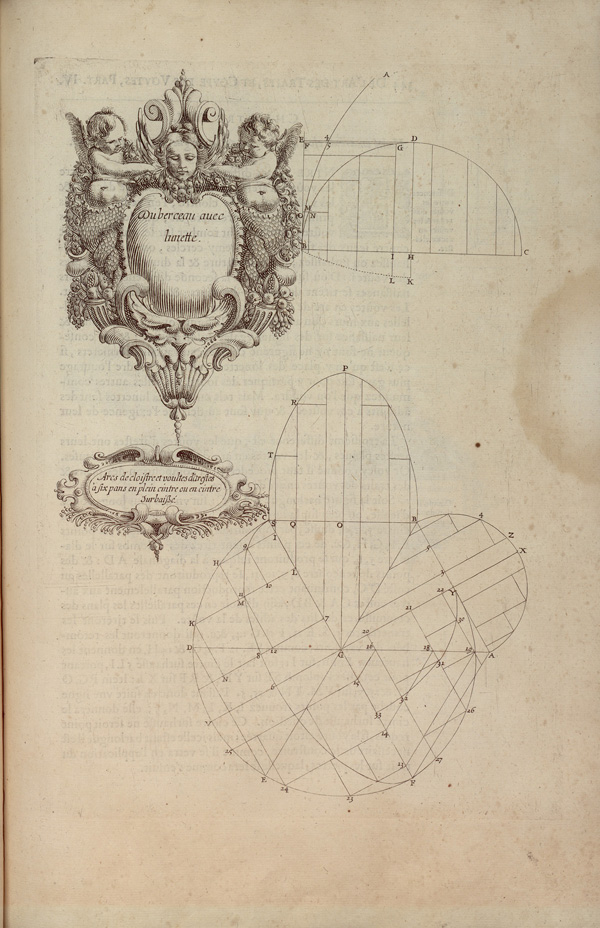
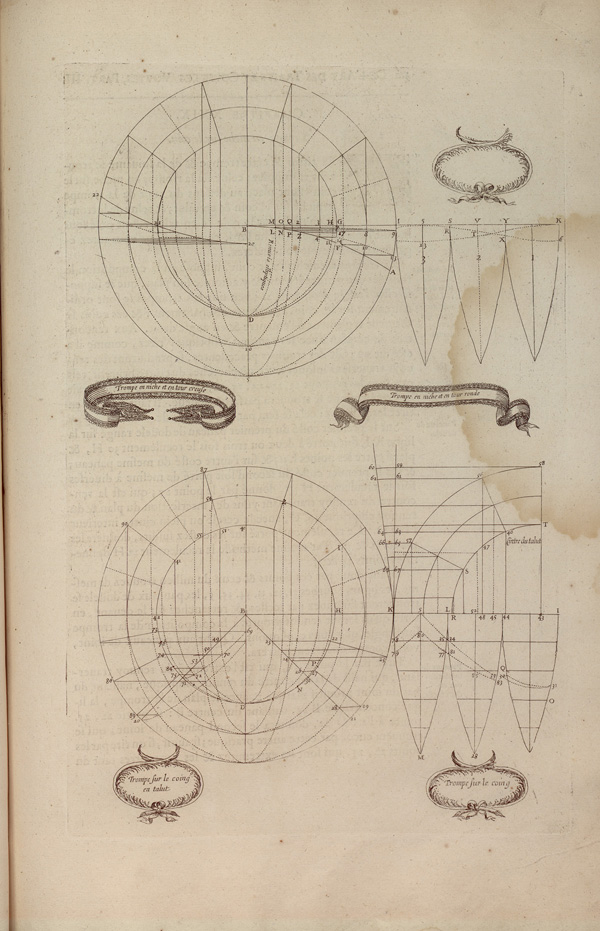
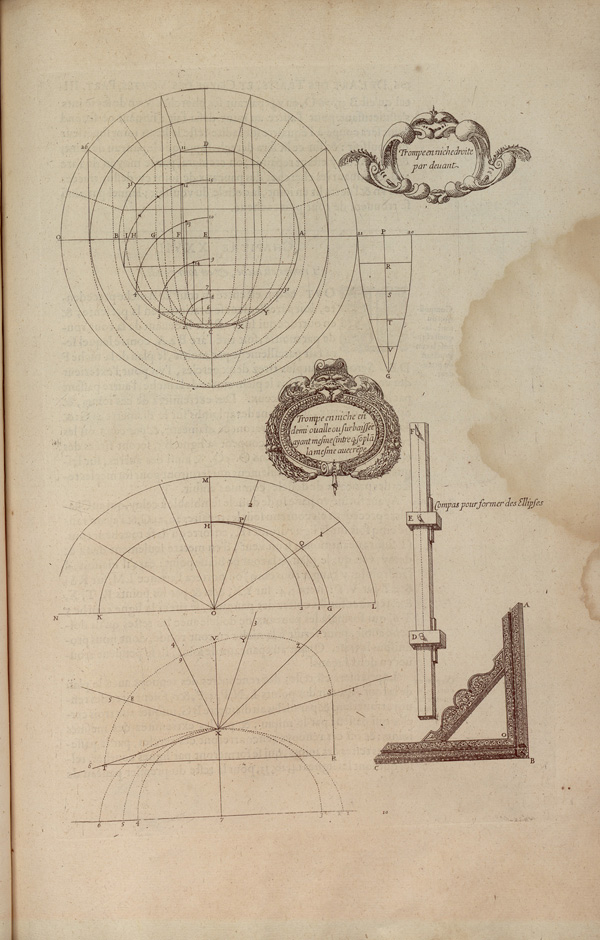
Philibert De l’Orme as early as 1561, in the Nouvelles inventions
Philibert De l’Orme describes how to use ordinates to draw the desired curve, but calls it curves lengthened and referrs to it as softening the curve.

All of Philibert De l’Orme ,1515, books at Open Archive

All of Mathurin b. Jousse, 1607, books at Open Archive

http://architectura.cesr.univ-tours.fr/Traite/Notice/ENSBA_Les1653.asp?param=en

Philibert De l'Orme septentrion boreas
As we can trace the foundations of a building by means of a perpendicular at the end of a straight line. CHAPTER I.
The invention to the bracket by means of a triangle came from Pythagoras, and he sees himself in the ninth book of Vitruvius, Chapter II. And serves as the triangle of lines and proportions only to that square, but also for many other things and other figures and geometrical instruments necessary and required to help construct buildings, and measure, I will not say the area, but all heights and widths, as I will show when he comes about.
Take the case that you have drawn the line QR, and hereunto an equilateral triangle, that is to say as great on one side than the other, as you see RST, T is the point where you pull another curved line marked Z, is tightened without moving the compass, and requires that the distance ST is similar to that of TZ. This makes you draw a straight line from point S to T, till it intersects the line Z, and this place, as you see the point marked X, you draw another line even to the point of R, which will be precisely perpendicular to the line QR, as you can judge by the figure followed.

In the first picture above, of the first speed square, Philibert De l'Orme developed it like a sundail.
French to English translation
LE PREMIER TOME DE L'ARCHITECTURE DE PHILIBERT DE L'ORME, 1567

Be given an equilateral triangle such width as you like, like ABC, the more it grows, so will the insurance and kindness. Where do I did not wish to help more than that which you see below figuratively, by as much as I used to be easier in my coffers, and do not usually point thereof, a Astrolable
be, and ephemeris, with a few other books, and cases filled compass, and what it takes to portraire. Within this triangle imagine a circle, as you can see marked EFGH (almost as if it were a dial showing the hours) and divide into so many parts that will, like twenty-four, thirty-two, forty eight, the most that there is the best.
I divided the latter into thirty-two, and is set amidst a magnetic needle, as well as marine dials and compasses, or small whom we help to find the hours to the Sun, but notice that said needle must be very good and very moving. When you want to help the triangle, you look through one side as you please, for the one marked in Figure D. This makes you discard your city view, castle or place from which you want to take the form and figure, and make a sketch first on paper scored coarsely and you can understand the decision. Can you make the trip at all. If you want that it should fit in memory or writing a bend and each face of the walls to measure the length as you will see below. Having done this, you can start at one end of the castle, town or place, keeping your triangle against the first section of wall with a ruler to have greater decision, against which must be your triangle as you see marked K. This makes you look at where does the needle, and how many, if ten or some other number, whatever it is, you mark the outline of your paper, right place cons which you presented your triangle. And after you go to another detour section of wall, and do as you did, with the rule and said your triangle against that section of wall, and looking at the number that stops the tip of the needle, which you also put on a sketch that was made to place all as before, and continue in this way all enceinture and around the city, or other place, but still marking to each piece of wall and bend the numbers on which the needle stop of your triangle, as I said, in a similar length that each contain a section of wall. All this well-ordered, when you want to make a fair level of your town or castle, you will extend over a table on paper or parchment on which you want portraire, being well bonded and attached around the edges. But you'll have the table farm, and can not turn here then at least just that this, that all lines of turn are drawn. Then you look at how many yards to your city in length and width and if there are a hundred or two hundred, we will divide into many parts numbers and the length of your paper, reducing them to small yards, for which you any measures to give your design that starts at one end, where to put the triangle where you are helped, and turn until the needle is exactly the number it was when you presented against the wall of the city. But do remember to put the lengths that you found each piece of a wall on their own place. This makes you pull the line throughout the side of your triangle D, which said triangle has been presented. For the better such a triangle must be made of any material that is not thick, like copper, brass, silver, or wood that hairline, so that it can easily take the above line, and has been accustomed to do with a ruler. You will present to the said triangle and to complete all other sections of wall, and turn till the needle is located exactly on the number to which it was when it was presented cons

Chancery building, Blois (Loir-et-Cher). 16th century. Philibert de l’Orme framework. Detail of the roofing: curved rafters and crown plates.
Philibert de l’Orme framework.

Drawings of Leonardo da Vinci
Geometrical construction of the Vitruvian Man by Leonardo da Vinci
Study of proportions, from Vitruvius's De Architectura , Vitruvian man
Studies of Concave Mirrors of Differing Curvatures, c. 1492

Rib vault From Wikipedia
http://en.wikipedia.org/wiki/Rib_vault

Groin vault From Wikipedia
http://en.wikipedia.org/wiki/Groin_vault

Centring From Wikipedia
http://en.wikipedia.org/wiki/Centring

German vaulting From German Wikipedia
http://de.wikipedia.org/wiki/Gew%C3%B6lbe

German rib vaulting From German Wikipedia
http://de.wikipedia.org/wiki/Gew%C3%B6lberippe

List of architectural vaults From Wikipedia
http://en.wikipedia.org/wiki/List_of_architectural_vaults

List of arch types From Wikipedia
http://en.wikipedia.org/wiki/Arch
http://www.artemisillustration.com/assets/text/Ornamental%20%20Terms_Glossary.htm

Hexagramm From German Wikipedia
http://de.wikipedia.org/wiki/Hexagramm

Peterborough Cathedral-The Complete Geometry 1100 – 1500
Canterbury Cathedral by COLIN JOSEPH DUDLEY
http://medievalarchitecturalgeometry.com/A3%20The%20Geometry.htm

Ad Triangulum (And maybe some Ad Quadratum too)
Timber Framers Guild
http://www.tfguild.org/forums/ubbthreads.php?ubb=showthreaded&Number=24132&PHPSESSID=9b674f8192c18c2d4f574afb5812f6d1

Designing With the Daisy Wheel
Timber Framers Guild
http://www.tfguild.org/forums/ubbthreads.php?ubb=showthreaded&Number=23838&PHPSESSID=855089735f286dc0b4aae183f8793dbc

Daisy wheel geometry
http://nicolawood.typepad.co.uk/kesurokai/daisy-wheel-geometry/

Designing with the daisy wheel
http://www.timberstructures.net/timber-framing.html

Doubling the Circle   - Sacred Geometry
http://dcsymbols.com/double_circle/double.htm

Nexus Network Journal
Pointed Arches
This gave inspiration of the static qualities of the equilateral triangle, well tested in Muslim architecture, and inspired the practical geometry (construction geometry) of Gothic Europe. The best pointed arch (with an inscribed equilateral triangle) has the geometry of the egg, which, being ruled by the Golden Number (accompanied by the number 3), determines a form that meets such conditions due to its being a system of great stability because of the harmony between its parts. The use in architecture of the geometric regularity of the bird's egg, in its paradigmatic form, besides satisfying aesthetical, constructive and economic conditions, allows the thrusts to be transmitted to the ground more directly and with minimal lateral efforts.

Arabic Euclidian architecture Pointed Arches

Nexus Network Journal
Didactics: Proportions in the Architecture Curriculum
Abstract.Roger Herz-Fischler presents a revised version of a chapter entitled "Proportions" that appeared in the problems part of his book,Space, Shape and Form /An Algorithmic Approach, developed for a mathematics course he taught in the School of Architecture at Carleton University from 1973-1984.
http://www.emis.ams.org/journals/NNJ/Didactics-RHF.html

Nexus Network Journal
Ad Triangulum
Transversal section of the Cathedral (Duomo) of Milan, from Cesariano's 1521 edition of Vitruvius (Plate LVI)
http://www.emis.ams.org/journals/NNJ/RHF-fig07.html

Nexus Network Journal
SPIRALS FROM THE GOLDEN RECTANGLE
Abstract.John Sharp examines spirals and the Golden Section for the Nexus Network Journal, Winter 2002.
http://www.emis.ams.org/journals/NNJ/Sharp_v4n1-pt02.html

Nexus Network Journal
The Geometer's Angle No. 6: R-Tiles
AbstractThe square root of the golden section, root-phi, is at times not given its due in discussions regarding the golden section. This is an unfortunate situation because the geometric properties of provide us with a unique and rarely applied design tool. In this column, geometer Mark Reynolds focuses on the root-phi rectangle and its abilities to create an exciting tiling, R-Tiles.
http://www.emis.ams.org/journals/NNJ/GA-v4n1-MAR.html

Nexus Network Journal 9,2: Architecture and Mathematics
By Kim Williams
http://books.google.com/books?id=pMvG5_H5wDUC&lpg=PA226&ots=LXe8-bIXQb&dq=The%20Book%20of%20Architecture%20of%20Hern%C3%A1n%20Ruiz&pg=PA228#v=onepage&q=The%20Book%20of%20Architecture%20of%20Hern%C3%A1n%20Ruiz&f=false

Nexus Network Journal About the ellipse:
It is true that ancient Greeks called the conics stereoi topoi (solid loci). However, they knew well the plane properties of these curves ( boast of Apollonius of Perga, 3rd-2th century B.C., but already partially known to Menecmo) . They did not have the mathematical tools to calculating the perimeter of the ellipse exactly (i.e., the elliptic integrals introduced in the works of Euler and Legendre ) but they could calculate the area of the ellipse (Archimedes, On Conoids and Spheroids, prop. 6, its approximation depending only on p ) . Apollonius's work was known during the Roman imperial age. The discovery of the gardener's method, namely a method to trace an ellipse by means of a rope string and two pivots, is attributed to Anthemius of Tralles (mathematician and one of the architects of Sancta Sophia). One can always suppose that this method is far older: according to some researchers it dates back to Neolithic age.
Why are Roman amphitheatres elliptical?

Vitruvius Scamilli -- Levelling Blocks

Translated and read with passion by the Renaissance humanists, the teaching of De architectura will overshadow much of the expertise of the builders of the Gothic period.
While the Romanesque liked the symbolism of numbers that referred directly to the biblical message and its interpretation, Gothic builders revere above all the geometry.
Article published in theEncyclopaedia Universalis, Corpus, January 1993, vol 2, pp. 843-851)

Joel Herschman - The Wise Master Builder: Platonic Geometry in Plans of Medieval Abbeys and Cathedrals

In all probability the Lombards are the originators of this device so pregnant of future possibilities. The new vault, groined, ribbed, and domed, was in a class by itself, apart from anything that had gone before. Particularly did it differ from the Roman vault in that, while the latter had a level crown, obtained by using semicircular lateral and transverse arches and elliptical groin arches (naturally formed by the intersection of two semicircular barrel vaults of equal radius), the "Lombard" vault was constructed with semicircular diagonals, the result being that domical form which was always retained by the Gothic builders of France because of its intrinsic beauty. Finally, the new diagonals suggested new vertical supports in the angles of the pier, and so we obtain the fully developed compound pier, which later, at the hands of the English, was to be carried to such extremes of beauty, and to form a potent factor in the development of the Gothic structural system.
Gothic Architecture

ANCIENT-WISDOM.CO.UK  Sacred Geometry
http://www.ancient-wisdom.co.uk/sacredgeometry.htm

Cathedrals around: the Word geometric, Thierry Champris, Editions Guy Trédaniel
The object of dispute was whether the elevation of the cathedral of Milan was, from the plan already in place, be drawn by regulators'ad quadratum"(as the square and octagon) or"ad triangulum"(as the triangle and the hexagon star / seal of Solomon).And was not so much about technique as a token, by the importance given to numbers by the Neoplatonic doctrines.
http://www.google.com/url?sa=t&source=web&cd=28&ved=0CDkQFjAHOBQ&url=http%3A%2F%2Fwww.paperblog.fr%2F2172245%2Fautour-de-cathedrales-le-verbe-geometrique-par-thierry-de-champris-editions-guy-tredaniel%2F&ei=HwbMTPbyKY24sQOyopn1Dg&usg=AFQjCNEEx9q9xSeZyTseLPPZl5yvhJdg8Q&sig2=GOEWlpIuShJzby3r7xuU7g Cathedrals: The verb geometric[Paperback] Amazon

France

  Price: £ 203.30
http://translate.googleusercontent.com/translate_c?hl=en&sl=fr&u=http://www.amazon.fr/gp/product/2844455565%3Fie%3DUTF8%26tag%3Dcompagnetcomp-21%26linkCode%3Das2%26camp%3D1642%26creative%3D6746%26creativeASIN%3D2844455565&prev=/search%3Fq%3DAd%2BTriangulum%26start%3D20%26hl%3Den%26newwindow%3D1%26sa%3DN%26rlz%3D1C1GGGE_enUS400US400%26prmd%3Divb&rurl=translate.google.com&twu=1&usg=ALkJrhgowz2F2eXiKUOSQtFE0VAt45rjNg
This looks like a good book, but 203 euros?
L e Compagnonnage
More about the book at compagnonnage.info  Stereotomique
www.compagnonnage.info| THE SITE OF RESEARCH OF JEAN-MICHEL MATHONIÈRE AND CENTRAL STUDY OF GUILDS

Cathedrals around: the Word geometric, Thierry Champris, Guy Trédaniel editions.
August 31, 2009
Cathedrals around: the Word geometric, Thierry Champris, Guy Trédaniel editions.
http://translate.google.com/translate?hl=en&sl=fr&u=http://compagnonnage.info/blog/blogs/blog1.php/2009/08/31/autour-de-cathedralesn-le-verbe-geometri&ei=HwbMTPbyKY24sQOyopn1Dg&sa=X&oi=translate&ct=result&resnum=9&ved=0CEQQ7gEwCDgU&prev=/search%3Fq%3DAd%2BTriangulum%26start%3D20%26hl%3Den%26newwindow%3D1%26sa%3DN%26rlz%3D1C1GGGE_enUS400US400%26prmd%3Divb
This web page is #1 in research on medieval free masons geometry
ANTÓNIO ROCHA FADISTA
The geometry of the Duomo was preserved in an edition of Vitruvius, published in 1521.
Röriczer Matthäus, a Freemason who has shown his art, breaking his oath of secrecy.Röriczer, who died in 1492, belonged to the third generation of a family of Master Masons who served in the Cathedral of Regensburg. Although being a Freemason, and was attached to the oath not to disclose the Masonic mysteries to the uninitiated, he took a big step with the publication of details previously hidden in the notebooks of Operative Masonic Lodges
http://translate.google.com/translate?hl=en&sl=pt&u=http://www.maconaria.net/portal/index.php%3Foption%3Dcom_content%26view%3Darticle%26id%3D4&ei=6AnMTOOgIoGusAP-z9CDDw&sa=X&oi=translate&ct=result&resnum=8&ved=0CD4Q7gEwBzge&prev=/search%3Fq%3DAd%2BTriangulum%26start%3D30%26hl%3Den%26newwindow%3D1%26sa%3DN%26rlz%3D1C1GGGE_enUS400US400%26prmd%3Divb

Chapter VI
A NEW ORDER IN SPACE ~
ASPECTS OF A THREEFOLD ORDERING OF
THE FUNDAMENTAL SYMMETRIES OF EMPIRICAL SPACE,
AS EVIDENCED IN THE PLATONIC AND ARCHIMEDEAN POLYHEDRA ~
TOGETHER WITH A TWOFOLD EXTENSION OF THE ORDER TO INCLUDE THE
REGULAR AND SEMI-REGULAR TILINGS OF THE PLANAR SURFACE
FIRST PUBLISHED IN THE INTERNATIONAL JOURNAL OF SPACE STRUCTURES, VOL. 6 NO.1,

UNIVERSITY OF SURREY, UNITED KINGDOM, 1991 (PREPARED IN RESPONSE TO THE EDITOR.’S INVITATION). ABSTRACT
There are generally considered to be five Platonic (Regular) and thirteen Archimedean (Semi-Regular) polyhedra (leaving aside the Kepler-Poinsot polyhedra, and disregarding the regular prisms and antiprisms).
http://web.me.com/rmeurant/INSTITUTE/Natural_Harmony_-_Essaying_Structural_Morphology_files/Ch-06-NewOrderInSpace.pdf

MYSTERIES OF THE EQUILATERAL TRIANGLE
Brian J. McCartin
http://www.m-hikari.com/mccartin-2.pdf

Chartres: the masons who built a legend, London,  by John James 1982,
http://www.johnjames.com.au/currentresearch-art-ge.shtml

Mathes Roriczer  Craft Secrets From Wikipedia
http://en.wikipedia.org/wiki/Mathes_Roriczer

Vitruvii De Architectura
http://www.vitruvius.be/inhboek1.htm

Stereotomy De quinque corporibus regularibus, De prospectiva pingendi, Vnderweysung der Messung mit den Zirkel un Richtscheyt
Art and science of cutting solids precisely so that their parts fit together tightly.
http://arts.jrank.org/pages/9896/Stereotomy.html

Piero della Francesca's Tetrahedron Formula
http://www.mathpages.com/home/kmath424.htm

Masion de l’Outil Tool and Trade Museum
http://www.maison-de-l-outil.com/index.php?page=accueil_anglais

Strictly speaking, the masterwork goes far beyond the accomplishment of a single compagnon. Most of the works that we admire today in museums are very large collective 19th-century works, designed to symbolically mark the supremacy of one guild group over another.
French compagnon master pieces

The first problem that faced medieval builders in the realization of vaults was how to cut the voussoirs constituting a structure. They seem to have answered this question from an essentially geometrical point of view, without taking statical or structural considerations into account. Indeed, stereotomy treatises illustrate the rules according to which voussoirs are to be cut in order to solve the different geometrical problems that may arise.
http://gilbert.aq.upm.es/sedhc/bibli.../CIHC1_017.pdf

A modern exercise in descriptive geometry, first done by German painter Albrecht Dürer. 21 May 1471 – 6 April 1528)
http://www.rarebookroom.org/Control/duruwm/index.html

The Edinburgh encyclopedia,
British system of projection
Peter Nicholson 1832 -- Freemason
Perspective is only a branch of the doctrine of solids; and all that this branch teaches, is only the methods for finding the sections of pyramids and cones, the eye being considered as the vertex, the original object the base of the pyramid or cone, and the picture to be drawn a section thereof; the term is there-fore of too general application, perspective being only a branch of stereography.

The eleventh and twelfth books of the Elements of Euclid belongs to stereography: these may be looked upon as the theory of the doctrine of solids, and to them we shall refer our readers for the original properties; but for their practical applications to useful practical applications in life, it is rather singular that so little has been done in this respect. The present article is entirely new. It is of the greatest importance in the various mechanical departments of architecture. The geometrical principles in masonry, carpentry, joinery, and the other useful branches of the building art, are entirely dependent upon it: in short, the cutting of individual pieces of timber in the art of carpentry, and the formation of separate stones in masonry, is only the application of stereography to practice.
http://www.archive.org/stream/edinburghencyclo05brew#page/n849/mode/2up

History of geometry
http://en.wikipedia.org/wiki/History_of_geometry

History of Descriptive Geometry in England
http://gilbert.aq.upm.es/sedhc/biblioteca_digital/Congresos/CIHC1/CIHC1_121.pdf

A Time Line of Mathematicians
A Time Line of Mathematicians

LES LIVRES D’ARCHITECTURE
Les Nouvelles Inventions pour bien bastir…
Philibert DeLorme (c. 1514 – January 8, 1570) was a French architect, one of the great masters of the French Renaissance.
He was born at Lyon, the son of Jean Delorme, a master mason. At an early age Philibert was sent to Italy to study (1533–1536) and was employed
http://architectura.cesr.univ-tours.fr/traite/Images/Masson643Index.asp
http://sites.google.com/site/delormearchitecture/

Charles-François-Antoine (1780-1854) - Treaty stereotomy : including the applications of descriptive geometry to the theory of shadows
Traité de stéréotomie : comprenant les applications de la géométrie descriptive à la théorie des ombres, la perspective linéaire, la gnomonique, la coupe des pierres et la charpente
http://gallica.bnf.fr/ark:/12148/bpt6k109545g.planchecontact.f21.pagination
http://gallica.bnf.fr/RequestDigitalElement?O=NUMM-109545&E=PNG&Deb=21&Fin=21&Param=D
http://gallica.bnf.fr/RequestDigitalElement?O=NUMM-109545&E=PNG&Deb=49&Fin=49&Param=D

Philibert Delorme
http://fr.wikipedia.org/wiki/Philibert_Delorme

Insights and considerations on the "network key"
Companions stonecutters of ancient Bauhütte
Des Compagnonnages (German)
http://translate.googleusercontent.com/translate_c?hl=en&sl=fr&u=http://www.compagnonnage.info/compagnons-tailleurs-de-pierre/reseaux.htm&prev=/search%3Fq%3DAd%2BQuadratum,%2BAd%2BTriangulum%26start%3D20%26hl%3Den%26newwindow%3D1%26sa%3DN%26prmd%3Divb&rurl=translate.google.com&twu=1&usg=ALkJrhhKhF_Brtoas7hIi0Kp59uQQvXqrA
Wooden churches in Romania
http://commons.wikimedia.org/wiki/Category:Wooden_churches_in_Romania

Tracing a Sacred Building Tradition
http://www.lub.lu.se/luft/diss/tec_797/tec_797.pdf
Note: the above link is 140MB... , but really neat timber framing in Romania

De Symmetria. . . and Underweysung der Messung- 1538 - Dürer, Albrecht (author) - Nuremberg - The Warnock Library
Rare Books
Page 113 seed of life, daisy wheel or just Euclidean geometry
http://www.rarebookroom.org/Control/duruwm/index.html

Elementa Geometriae- 1482 - Euclid, (author) - Venice - The Bancroft Library; University of California, Berkeley
Rare Books
http://www.rarebookroom.org/Control/eucgeo/index.html

Descriptive geometry, as applied to the drawing of fortification and sterotomy. For the use of the cadets of the U.S. Military academy (1864)
Mahan, D. H. (Dennis Hart), 1802-1871
http://www.archive.org/stream/descriptivegeom02mahagoog#page/n75/mode/1up

BOOKS ON ARCHITECTURE
http://architectura.cesr.univ-tours.fr/traite/matiere.asp

Derand, Francis (1588? -1644)
The architecture of arches, or the art features and cutting vaults ..., Par is, Sebastien Cramoisy, 1643.
http://architectura.cesr.univ-tours.fr/traite/Notice/B250566101_11598.asp?param=

Creating Shapes in Civil and Naval Architecture: A Cross-Disciplinary Comparison
By Horst Nowacki, Wolfgang Lefèvre
Page 302 http://books.google.com/books?id=8FoHYXEwAXEC&lpg=PP1&pg=PA108#v=onepage&q&f=false

Stereotomy, construction,stone-cutting(1567-2002)
http://www.arch.unige.it/bma/ENGL/engl_biblio_stereo_crono.html

The trunk of the street in Paris Larivière
http://translate.google.com/translate?hl=en&sl=fr&u=http://compagnonnage.info/blog/blogs/blog1.php/2009/10/05/trompe-rue-lariviere-paris&ei=E1TLTP6XKYe8sAOEsOTQDg&sa=X&oi=translate&ct=result&resnum=2&sqi=2&ved=0CB8Q7gEwAQ&prev=/search%3Fq%3Dtrompe%2Bde%2Bla%2Brue%26hl%3Den%26newwindow%3D1%26rlz%3D1C1GGGE_enUS400US400%26prmd%3Div
The Construction of Gothic Cathedrals byJohn Fitchen
http://books.google.com/books?id=KI3dJzP0p00C&printsec=frontcover&dq=The+Construction+of+Gothic+Cathedrals+by+John+Fitchen&source=bl&ots=5QbsncAK7E&sig=kObljaXP_pDy2l5MDh5fwWIV3dk&hl=en&ei=aDLMTOW_N5KCsQO2tezQDg&sa=X&oi=book_result&ct=result&resnum=1&ved=0CBsQ6AEwAA#v=onepage&q&f=false
The New Metal Worker Pattern Book | by George Watson Kittredge 1901
Problem 146. Pattern Of A Tapering; Article With Equal Flare Throughout, Which Corresponds To The Frustum Of A Cone Whose Base Is An Approximate Ellipse Struck From Centers, The Upper Plane Of The Frustum Being Oblique To The Axis
http://chestofbooks.com/crafts/metal/Metal-Pattern/Problem-146-Pattern-Of-A-Tapering-Article-With-Equal-Flare-Throughout-Which-C.html

Apollonius on conic sections from ~200 BC
http://www.archive.org/stream/treatiseonconics00apolrich#page/n9/mode/2up

Villard deHonnecourt’s notebooks.
Gaspard Monge, no Freemason tattler, who wrote about "Descriptive Geometry, or the Art & Sciece of Masonic Symbolism."

Carpentry and building, Volume 13 1891

MASONRY AND STONE CUTTING
http://books.google.com/books?id=AXoAAAAAYAAJ&lpg=PA142&ots=78BexfwVNM&dq=conoid%20%20vault&pg=PA111#v=onepage&q=conoid%20%20vault&f=false

Călineşti Susani church sun rosette or Thunder rosette
http://en.wikipedia.org/wiki/C%C4%83line%C5%9Fti_Susani_church

Reconstructing Architectural Geometry
Earl Mark, Ph.D.
Associate Professor of Architecture
University of Virginia
http://www.re-h.nl/koutamanis/image05/mark/arqpapCMP.pdf

Wood carving in churches in Romania
http://commons.wikimedia.org/wiki/Category:Wood_carving_in_churches_in_Romania

Gothic Cathedral and Church Construction
http://www.abelard.org/france/cathedral-construction.php

Schneider, Mark. "Self-Invention and Deviance: Philibert de l'Orme's Role in the Creation of the Savant Professional Architect."Discoveries25.1 (2008). 24 June 2008.
Le Premier Tome de l’architecture
trompes(ribless, conical vaults)
http://cstl-cla.semo.edu/reinheimer/discoveries/archives/251/schneider251pf.htm

Abstract.Roger Herz-Fischler presents a revised version of a chapter entitled "Proportions" that appeared in the problems part of his book,Space, Shape and Form /An Algorithmic Approach, developed for a mathematics course he taught in the School of Architecture at Carleton University from 1973-1984.
http://www.emis.de/journals/NNJ/Didactics-RHF.html

The Role of the Master Mason in Mediaeval English Building
L. R. Shelby
Vol. 39, No. 3 (Jul., 1964), pp. 387-403
(article consists of 17 pages)
Published by:Medieval Academy of America
Stable URL: http://www.jstor.org/stable/2852495
Ad Quadratum Construction and Study of the Regular Polyhedra by Jean Le Mée

http://www.gatewaycoalition.org/files/millennium_sphere/products/AdQuadratum.pdf
TECHNICAL DRAWING (2) The first half of the 19th century might well be called a formative period in the development of technical drawing. Durer (1471-1528) was credited with the first basic knowledge of orthogonal/orthographic projection.
But nothing was published until 1795 when a book written by Gaspard Monge, 'La Geometries Descriptive'.

http://www.gr8lessons.com/history/TechDraw2.html
A history of Western architectureBy David Watkin Kuttenberg Cathedral

http://books.google.com/books?id=39T1zElEBrQC&lpg=PA191&ots=70RMTe6q_i&dq=st%20anne%20annaberg%20vaulting&pg=PA192#v=onepage&q&f=false

A history of architecture in all countries from the earliest times ..., Volume 2
By James Fergusson Saint Barbara Kuttenberg
http://books.google.com/books?id=ENgDAAAAYAAJ&lpg=PA74&ots=aZG1AjCAGS&dq=Saint%20Barbara%20Kuttenberg&pg=PA136#v=onepage&q&f=false

Centralblatt der Bauverwaltung, Volume 8 Saint Barbara Kuttenberg
http://books.google.com/books?id=PJkAAAAAMAAJ&dq=Saint%20Barbara%20Kuttenberg&pg=PA100#v=onepage&q&f=false

Marcus Vitruvius Pollio:de Architectura, Book I
ichnography, orthography, and scenography
Arises out of dimension(quantitas)
The form of a theater is to be adjusted so that from the center of the dimensionless allotted to the base of the perimeter is a circle to be described, in Which are inscribed four equilateral triangles, at equal distances from each other, Whose points are to touch the circumference of the circle.This is the method that is practiced by astrologers in describing the twelve celestial signs, according to the musical division of the constellations.Of these triangles, the side of That which is nearest the scene will Determine the face thereof in that part where it cuts the circumference of the circle.Then the center is a line drawn through parallel to it, Which Will separate thepulpitumof theprosceniumfrom theorchestra.
http://translate.googleusercontent.com/translate_c?hl=en&sl=de&u=http://penelope.uchicago.edu/Thayer/E/Roman/Texts/Vitruvius/1*.html&prev=/search%3Fq%3Dalso%2BMarcus%2BVitruvius%2BPollio,%2BVitruvii%2BDe%2BArchitectura%2B-chpt%2B8%26hl%3Den%26newwindow%3D1%26prmd%3Divb&rurl=translate.google.com&twu=1&usg=ALkJrhicxjKBP8UiP-k09rXBkCx0-z43-A

Cistercian benedictine monks
Constantine the Great
Hagia Sophia
Byzantine architecture
Constantinople
Basilica Cistern 336 columns in 12 rows,
http://www.arkeo3d.com/byzantium1200/introduction.html
The intersection of cylinders (i.e. a groin vault) was first analysed precisely byPiero della Francesca(c.1415–92) in his worked example for Problem X inDe quinque corporibus regularibus, and their perspectival representation inDe prospectiva pingendi(II and XI).Albrecht Dürer(1471–1528) introduced Euclidean geometry to northern artists inVnderweysung der Messung mit den Zirkel un Richtscheyt(1525), which became more accessible outside Germany in a Latin translation,Institutiones Geometricae(Paris,1538).

Abstract.Answers to a reader's query about the origin and symbolic significance of pointed arches, in the Nexus Network Journal.
http://www.emis.de/journals/NNJ/Query01-PointedArches.html

Euclid’s Elements Book 1 Prop 1
To construct an equilateral triangle on a given finite straight line.
http://aleph0.clarku.edu/~djoyce/java/elements/bookI/propI1.html

Knights Templar Sinclair
http://www.rosslyntemplars.org.uk/index.php/sinclairs/

The construction of Gothic cathedrals: a study of medieval vault erection
By John Fitchen
http://books.google.com/books?id=KI3dJzP0p00C&lpg=PA42&ots=5QbrpdEF8C&dq=medieval%20cathedral%20vaulting&pg=PA57#v=onepage&q=medieval%20cathedral%20vaulting&f=false
Tiles as a substitute for steel: the art of the timbrel vault
http://www.lowtechmagazine.com/2008/11/tiles-vaults.html

Perspective versus Stereotomy: From Quattrocento Polyhedral Rings to Sixteenth-Century Spanish Torus Vaults  José Calvo-López
http://www.springerlink.com/content/3347m764427x4230/fulltext.pdf

Dürer himself called the ellipse “the egg line” (eyer lini).
http://pavlopoulos.wordpress.com/2009/07/27/albrecht-duerers-eyer-lini/

Guldin in 1640 who discovered the elliptical nature of the curve
A treatise on the teeth of wheels:Demonstrating the best forms which can be given to them for the purposes of machinery, such as mill-work and clock-work
http://books.google.com/books?id=-5FKAAAAMAAJ&lpg=PA144&ots=crRqxNmgWQ&dq=treatise%20of%20geometry%20Charles-%C3%89tienne-Louis%20Camus&pg=PA121#v=onepage&q&f=false

Marcus Vitruvius Pollio:
De Architectura, Liber III
Chapter 1
3rd
Just so the parts of Temples should correspond with each other, and with the whole. The navel is naturally placed in the center of the human body, and, if in a man lying with his face upward, and his hands and feet extended, from his navel as the center, a circle be described, it will touch his fingers and toes. It is not alone by a circle, that the human body is circumscribed Thus, as may be seen by placing it within a square. For measuring from the feet to the crown of the head, and then across the arms fully extended, we find The latter measure equal to the former, so that lines at right angles to each other, enclosing the figure, will form a square. º
vero similiter sacrarum aedium membra ad Universam summam ex partibus singulis totius magnitudinis convenientissimum debent habere commensus responsum. item centrum corporis medium naturaliter est umbilicus. inamque si fuerit homo conlocatus supinus manibus et Pedibus pansis circinique conlocatum centrum eius in umbilico, circumagendo rotundationem utrarumque manuum et digiti pedis linea tangentur. non minus quemadmodum schematic rotundationis in corpore efficitur, item quadrata designatio in eo invenietur. nam si ad summum caput a Pedibus imis mensum erit eaque mensura relata ad manus fuerit Panza, invenietur latitudo uti eadem altitudo, quemadmodum Areae quae sunt ad normam quadrata.
Vitruvius Book 6
Properties of two famous amphitheatres : the Colosseum(Rome) and the Arena(Verona)
Elliptical Colosseum

The Sambuca is a elliptical curve with ordinates or a triangular harp
Sambuca

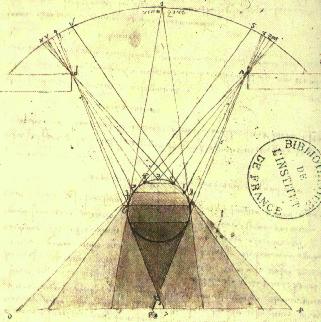
gnomon,menaeus,ecliptic, analemmas, elliptical trace on an analemmatic sundial,16th century works of Oronce Fine, shadow length of the gnomon, the hectemoros circle
Vitruvius' analemma, Ptolemy's anaemma, water clocks (clepsydras)

The menaeus rotated edge-on is shown, then two edge-on and one facing ecliptic circles oriented at different angles relative to the menaeus but having the same diameter projection. We can drop perpendiculars to the diameter LH to find the sun circles
The Analemmas of Vitruvius and Ptolemy
Vitruvius Pollio and the Analemma
orthographic projection
The graphical construction called the épure in France for the design of sundials is a similar procedure.
The analemma was also a kind of armillary sphere used for spherical trigonometry by Ptolemy

Roman engineers used a method of graphical computation and design that was very much in the style of Monge's descriptive geometry of the 19th century, until recently taught to every engineering student. This procedure makes use of two or more views, each showing two dimensions, and the combination showing all three dimensions necessary to describe a body in space. Vitruvius would probably have made his views overlap, in spite of the confusion of lines that results, to save space. We shall separate the two views in the modern manner so that each can be appreciated alone. The graphical construction called the épure in France for the design of sundials is a similar procedure.
Vitruvius Pollio and the Analemma

The orthographic projection was known by the Egyptians and Greeks 2000 years ago. Azimuthal Projections

41 BC -- The Roman architect Vitruvius (Marcus Vitruvius Pollio) includes information on sundials in his "De Architectura" on engineering and architecture. He uses the word analemma in referring to a form of orthographic projection.
orthography: the art of drawing anything without perspective, as though viewed from infinity. In dialling, the sphere so drawn consists of circles, straight lines and ellipses. Hence orthographic (or orthogonal) projection, which is used in the universal astrolabe.
analemmatic dials consisting of hour points, (rather than lines) laid round an ellipse

Regiomontanus, Apian and Capuchin Sundials
Regiomontanus, Apian and Capuchin Sundials
Capuchin Friar
Analemmatic sundial by plotting abscissas and ordinates. Analemmatic Dial. Motto: The Light and Shadow of God
Analemmatic sundials: How to build one and why they work
The analemmatic sundial is based on an ellipse which is marked out in hour points
An ellipse is an example of a curve called a conic section. Other conic sections are the circle, the parabola and the hyperbola. The Earth travels around the sun on an elliptical path.

Analemmatic sundials
umbra recta: Latin for "upright shadow", it is the label often found on the cotangent scale of altitudes < 45º on a shadow square.
umbra versa: Latin for "reverse shadow", it is the label often found on the tangent scale of altitudes > 45º on a shadow square.
Basic sundial nomenclature
umbra recta -- the shadow cast by a horizontal stick on a vertical surface
umbra versa -- the shadow cast by a vertical stick on a horizontal surface
Quadrato geometrico per misurare ogni lunghezza (geometrical square to measure every length) 60
Scala altimetra di gradi 100 per misurare ogni altezza da lontano (Altitude scale of 100 degrees, to measure every far height) 12 .

The Shadow Square
The shadow square, also called altitude scale, generally placed on the back of astrolabes and quadrants, is the basic element of the so-called geometrical square. The instrument serves to measure heights and distances by simulating the ratio between a gnomon and its shadow. The umbra recta simulates the shadow cast on the horizontal plane by a vertical gnomon when the Sun's ray is inclined between 0° and 45°. The umbra versa simulates the shadow cast on the vertical plane by a horizontal gnomon when the Sun's ray is inclined between 45° and 90°. To each value of the umbra recta corresponds a value of the umbra versa. When the ray is inclined by 45°, the two shadows are equal (umbra media).

"Ecliptic" simply means "(oblique) circle" (in Greek ekklitiké, from klinein = to bend)
Claudius Ptolemaeus (Ptolemy) epicycles
Claudius Ptolemaeus (Ptolemy) Apotelesmatika -Quadripartitum (four books) of astrological treatise
CHRONOLOGY – some selected dates in the development of sundials and solar astronomy
development of sundials and solar astronomy
Analemmatic Dial. Motto: The Light and Shadow of God
Analemmatic sundial by plotting abscissas and ordinates. The point (3,2) has 3 as its abscissa (x) and 2 as its ordinate (y).
Drive the chariot of the sun’s arc south of the equator to see the chariot of light at winter solstice.

Azimuthal Projections
Equatorial orthographic map, central meridian 70°E It is remarkable that some azimuthal projections, important even today, were known more than two thousand years ago by the Greeks and maybe by the Egyptians. The orthographic, stereographic and gnomonic projections are all based on solid principles of perspective and Euclidean geometry, while the azimuthal equidistant dates from the 15th century and is constructed arbitrarily.
Mentioned by the Greek Hipparchus in the 2nd century B.C., but probably known earlier, the azimuthal orthographic (usually simply referred to as the orthographic) projection was called analemma by Ptolemy and got its modern name from d'Aiguillon (1613).
Map Projections

mubattakh == melon shape, flatten mubattakh -- ellipse orthographic projection
reconstruction of Al-Birunis Cylindrical Projection -- 442 AD
Islam Anaphoric clock dials -- Astrolabe
Cartography in the traditional Islamic , map making
The history of cartography: Cartography in the traditional ..., Volume 2, Book 1 edited by J. B. Harley, David Woodward

AXONOMETRIC PROJECTION
The Greek word axon means axis and metric means to measure. Axonometric projection is a parallel projection technique used to create pictorial drawings of objects by rotating the object on an axis relative to a projection plane to create a pictorial view.
Axonometric drawings are classified by the angles between the lines comprising the axonometric axes.
AXONOMETRIC PROJECTION

Taprats is a Java applet that implements one such design technique for Islamic star patterns for polygons tiling.
Taprats Computer Generated Islamic Star Patterns
Islamic star patterns Java Applet

six-point geometry, eight-point geometry, ten-point geometry, twelve-point rosettes,fifteen-point rosette, Islamic geometric design,
Distinct from sacred geometries is geomancy, a tradition of divination, but which has a tradition in the Arabic and other worlds with a relationship with numbers, not geometry. The divination is composed of two elements: numbers and a body of knowledge governing interpretation. The only reason I mention it here is that some believe there is a relationship between geomancy and mathematics and, by extension, astrology and cosmology to which sacred geometries, as I’ve mentioned, relate.
Here the same basic construction has been developed in order to produce a shape with six pointed foils – a hexafoil or sexfoil.
Arabic geometry,the basic seven-circle rose from the six-point geometry
based on eleven-point geometry. The hendecagon, or eleven-sided figure, has internal angles of 147·2727…°.

Hexagram
mandala , [Skt.,=circular, round] a concentric diagram , Sacred Islamic Geometry grows from a circle
star of David or Solomon's seal

The works of Euclid and Pythagoras were among the first to be translated into Arabic.
The rules of construction of geometric patterns provide a visual analogy to religious rules of behavior
The circle, and its centre, are the point at which all Islamic patterns begin.
From the circle comes three fundamental figures in Islamic art, the triangle, square and hexagon. The triangle by tradition is symbolic of human consciousness and the principle of harmony. The square, the symbol of physical experience and the physical world-or materiality-and the hexagon, of Heaven. Another symbol prevalent in Islamic art is the star and has been the chosen motif for many Islamic decorations. In Islamic iconography the star is a regular geometric shape that symbolizes equal radiation in all directions from a central point. All regular stars -- whether they have 6, 8, 10, 12, or 16 points -- are created by a division of a circle into equal parts. The center of the star is center of the circle from which it came, and its points touch the circumference of the circle. The rays of a star reach out in all directions, making the star a fitting symbol for the spread of Islam.
ISLAMIC PATTERNS & GEOMETRY

Railroads and Skew Vaults
The difficulty of constructing skewed vaults led to interesting solutions in Gothic architecture, as John Fitchen shows in his book The Construction of Gothic Cathedrals: A Study in Medieval Vault Erection. Similar problems arose in the nineteenth century, when “the advent of railroads demanded bridges of arched masonry many of which had to accommodate a right-of-way that crossed a stream or a roadway at an oblique angle.”

The shapes of the groin voussoirs, if properly cut to key accurately into the web stones of the two vault surfaces whose intersection they form, are very difficult to arrive at. This difficulty unquestionably accounts for the very small number of unribbed, simple groin vaults constructed by the medieval builders over naves. They could “get away with” approximate shapes
Islamic Art and the Argument from Academic Geometry

10th century treatise "On Those Parts of Geometry Needed by Craftsmen" by the famous Persian mathematician Abul Wafa al-Buzjani at Baghdad
Islamic Constructions: The Geometry Needed by Craftsmen
Geometric Constructions and their Arts in Historical Perspective
The Circle for Iranian Architectural Studies
Spherical tetrahedron, Tiling with six spherical squares, Construction of Some Spherical Archimedean Solids
An Introduction to Medieval Spherical Geometry for Artists and Artisans

The apothem of a regular polygon is the distance from center to the midpoint of a side. It is also the radius of the inscribed circle. Only regular polygons have an apothem.
Platonic solids

Another important work in Islamic geometry was Apollonios of Perga's The Conics from about 200 BC. Though The Conics contained eight chapters or books, only four exist in Greek and only seven in Arabic. These three Greek scholars -- Euclid, Archimedes, and Apollonios -- formed the basis of Islamic mathematics. Muslim mathematicians and translators are responsible for the preservation and transmission of these texts through the medieval period.
Islamic geometry History
Ibrahim ibn Sinan ibn Thabit ibn Qurra (d. 946), On Drawing the Three Conic Sections

BULDING SIMPLE SUNDIALS

When a right triangle is rotated about the X-axis, it forms a cone with its axis of symmetry as the same X-axis.

Isometric Projection

three centered elliptical, five centred elliptical arch
Definition of the Ellipse

The important thing to remember is that conic sections in Roman times were all defined as cuts of cones; equation forms did not exist! So laying out an elliptical field is something that may not have even entered someone's mind.

Stereographic projection
Earliest known uses were in Greece for map making Earliest references in literature (Roman, ~100 B.C.) Vitruvius ~ Ten Books on Architecture Ptolemy’s ~ Representation of the Sphere in the plane

Building age, Volume 10 -- 1888

 

What is this geometrical symbol in Roncesvalles?

2* pi *height = perimeter of pyramid
1/2 * base * apothem = phi
The Great Pyramid, The Great Discovery, and The Great Coincidence

The Great and second Great Pyramid Geometry

Knights Templar tombstone from St Magnus cathedral in Kirkwall
1118 Knights Templar Founded in Jerusalem, at the site of Solomon's Temple.
845 Saint Clair Eventual namesake of the Sinclair family is born.
Knights Templar tombstone from St Magnus cathedral in Kirkwall

History of Building construction 60,000 BC to 1000 BC History of Building construction
History of Building Greece Log Motif

The Way of the Japanese Carpenter: Tools and Japanese Architecture. by William H. Coaldrake
Chris Hall Tressle Saw Horse
Traite Theorique Et Pratique De Charpente by Louis Mazerolle(1889) and Art Du Trait Pratique De Charpente by Emile Delataille
Chris Hall Emile Delataille
Who is Emile DELATAILLE

 

Title : Traité de stéréotomie : comprenant les applications de la géométrie descriptive à la théorie des ombres, la perspective linéaire, la gnomonique, la coupe des pierres et la charpente, avec un atlas composé de 74 planches in-folio. II. Atlas. - In-fol., 74 pl. / par C.-F.-A. Leroy,...
Author : Leroy, Charles-François-Antoine (1780-1854)
Publisher : Gauthier-Villars (Paris)
Date of publication : 1877
Contributor : Martelet, Émile (1805-18..). Éditeur scientifique. Annotateur
Subject : Géométrie descriptive
Subject : Stéréotomie
Type : monographie imprimée
Language : French
Format : 2 vol. : fig. ; in-4, in-fol.
Format : application/pdf
Copyright : domaine public

Traité de stéréotomie for charpente

Good book on stereotomic geometry by Leroy, Charles-François-Antoine
Traité de géométrie descriptive

Traité de géographie descriptive By Jules De La Gournerie

 

a corona ("crown") and cyma ("ogee") molding to support the projecting roof.
2. For the human body is so designed by nature that the face, from the chin to the top of the forehead and the lowest roots of the hair, is a tenth part of the whole height; the open hand from the wrist to the tip of the middle finger is just the same; the head from the chin to the crown is an eighth, and with the neck and shoulder from the top of the breast to the lowest roots of the hair is a sixth; from the middle of the breast to the summit of the crown is a fourth. If we take the height of the face itself, the distance from the bottom of the chin to the under side of the nostrils is one third of it; the nose from the under side of the nostrils to a line between the eyebrows is the same; from there to the lowest roots of the hair is also a third, comprising the forehead. The length of the foot is one sixth of the height of the body; of the forearm, one fourth; and the breadth of the breast is also one fourth. The other members, too, have their own symmetrical proportions, and it was by employing them that the famous painters and sculptors of antiquity attained to great and endless renown.
http://www.crystalinks.com/greekarchitecture.html